UPC EETAC Bachelor's Degree in Telecommunications Systems and in Network Engineering EEL

L3.1

Lecture 2

L3.2: Plan C2 and circuit expandability (circuit scalability)

[P3] n-bit arithmetic circuits

L3.3

[4/3]

1.9.1.2. n-bit adder

1.9.1.2.1. Ripple-carry adder: Adder_4bit, Adder_8bit

This tutorial shows how to design an Adder_4bit using Adder_1bit blocks. The key idea in this lecture is discussing the plan C2 internal architecture and study its direct translation to Adder_4bit.vhd (coloured pdf printing; here is explained how to do it):

Circuit Translation

1.9.1.3. Commercial standard adder chips in classic technologies

This is a commercial standard 4-bit adder  Adder_4bit 74HCT283. It is based on carry lookahead (CLA) equations plan A architecture as shown in tutorial Adder_4bit.

 

1.9.2.2. n-bit comparator (Comp_4bit, Comp_8bit, etc.)

The idea on how to organise a larger comparator, for instance Comp_6bit, is based on using auxiliary inputs Gi, Ei, Li to allow cascading circuits of the same kind.

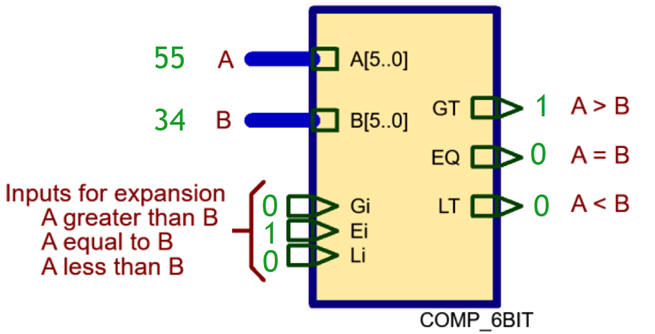
Comp_6bit

Comp_6bit can be invented using these two approaches shown  below where Comp_4bit or Comp_3bit can be implemented using Comp_1bit:

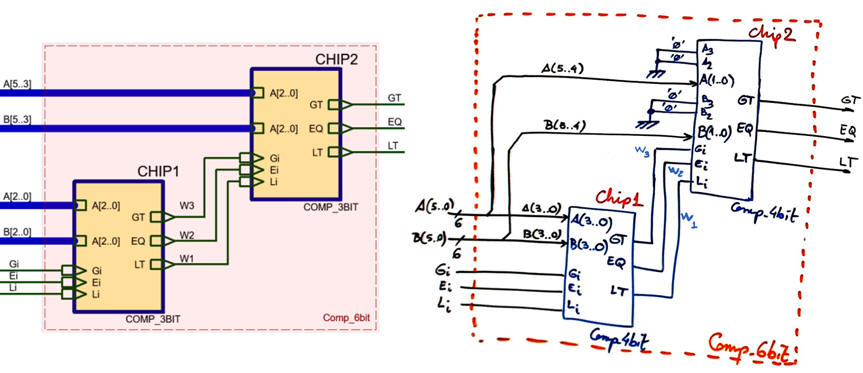
Comp_6bit_planC2

In this way, other comparator tutorial projects can be found: Comp_4bit, Comp_10bit chaining Comp_1bit components.

 

1.9.2.3. Commercial standard comparator chips in classic technologies

Commercial standard 4-bit comparator Comp_4bit 74F85. It is based on plan A equations as shown in this tutorial Comp_4bit.

 

1.9.3.2. n-bit multipliers

Mult_8bit. and Mult_9bit.

1.9.4. Counting the number of ones in a n-input vector: Ones_counter_nbit

1.9.4.1. Ones_counter_4bit

Counting the number of ones in a given data vector:  Ones_counter_4bit. This is the typical application for counting the number of free slots in a parking.

1.9.4.2. Ones_counter_8bit.

This project is highlighted in P3: Ones_counter_8bit.

 

Indeed, most standard circuits may be inferred in the same way using modular hierarchical structures and repeatable building blocks (plan C2). This is the idea of circuit expandability or scalability proposed as a concept at the mind map. Some examples for both, arithmetic and logic circuit types:

Circuit using plan C2 Building blocks
MUX_8 Mux_2 and MUX_4
Octuple_Mux_4 Mux_2
Dec_4_16 Dec_2_4
Enc_10_4 Enc_4_2
Adder_4bit, Adder_1bit
Adder_8bit Adder_1bit, Adder_4bit
Comp_6bit Comp_4bit, Comp_1bit
Mult_4bit Mult_1bit
Ones_counter_8bit Ones_counter_4bit

The same concept of circuit expandability will be used in Chapter 2 on the design of counters, memories, registers, etc.

 

Exercise on arithmetic operations: Perform the following operations in radix-2

S = (345)10 + (677)10 

S = (879)10 -  (234)10 

S = (87)10  x (34)10 

 

Compare A = (817)10 ; B = (332)10 

 

Exercise: on circuit expandability: Invent a MUX_16 using  a hiearchical design based on MUX_4 components.