UPC EETAC Bachelor's Degree in Telecommunications Systems and in Network Engineering EEL

L3.3

Lecture 1

L4.1: Integer arithmetic in 2C

[P4] Two's complement (2C) arithmetic for signed integer numbers

L4.2

[8/10]

1.10. Integer arithmetic

Let us start with symbols because they are an important tool to clarify what is expected from an arithmetic circuit and what data it will use.

Typical symbols for radix-2 (unsigned) numbers, already designed in P3 (Visio).

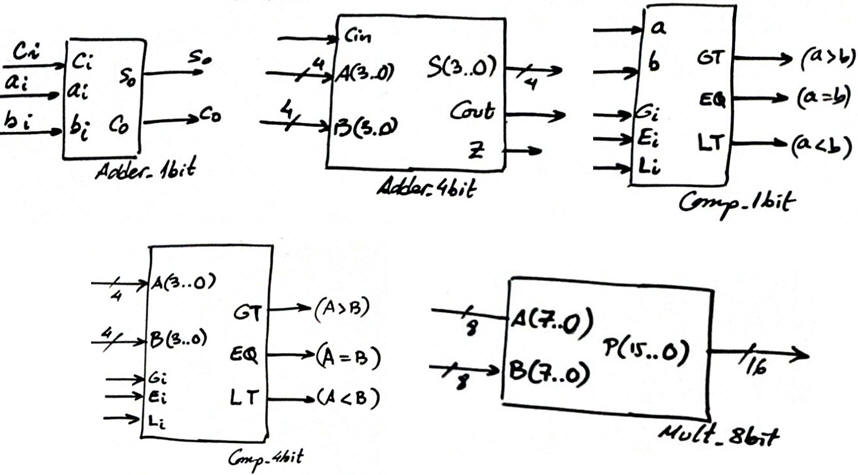
radix-2 circuits

Typical symbols for integer (signed) numbers.

Circuits for signed arithmetics

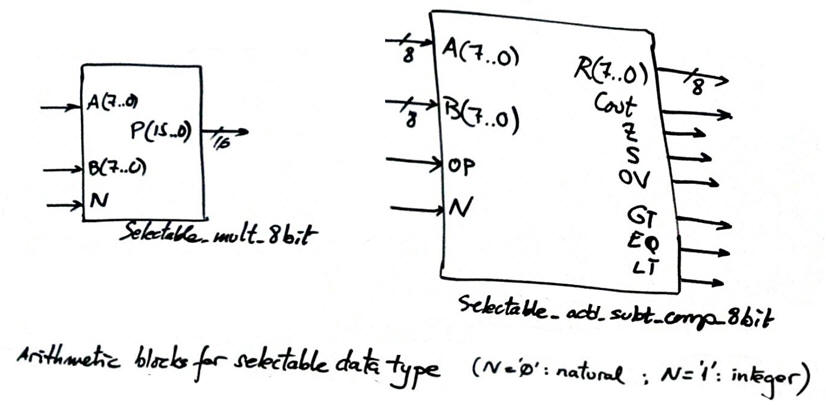
Typical circuits that can operate two data types: when N = '0' unsigned (radix-2) and when N = '1' signed integers.

selectable circuits

1.10.1. Integer number two's complement (2C) representation

The key point is how to represent positive/negative numbers (integers): two's complement (2C) convention and range of values for a given number of N bits.

Represent several positive and negative numbers in two's complement and operate additions and subtractions.

Twos complement

how to generate two complement numbers

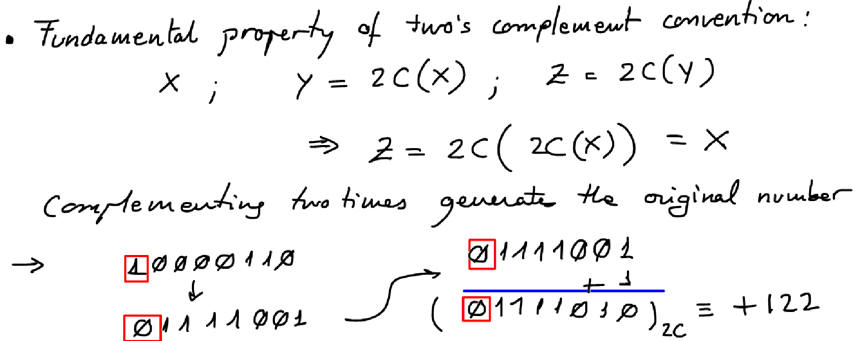
Fundamental property

Additions in 2C numbers:

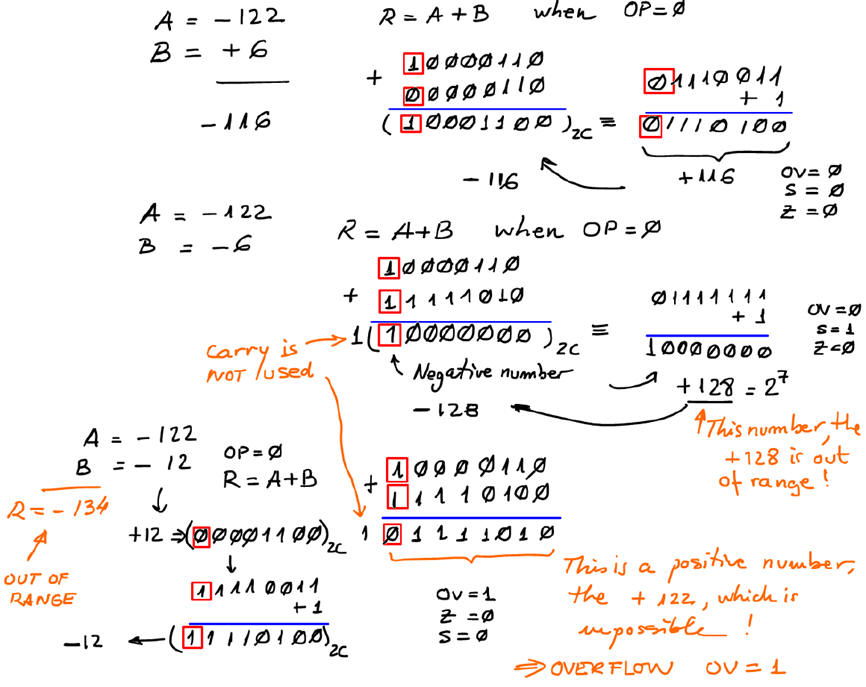
Additions in 2C

Subtractions in 2C:

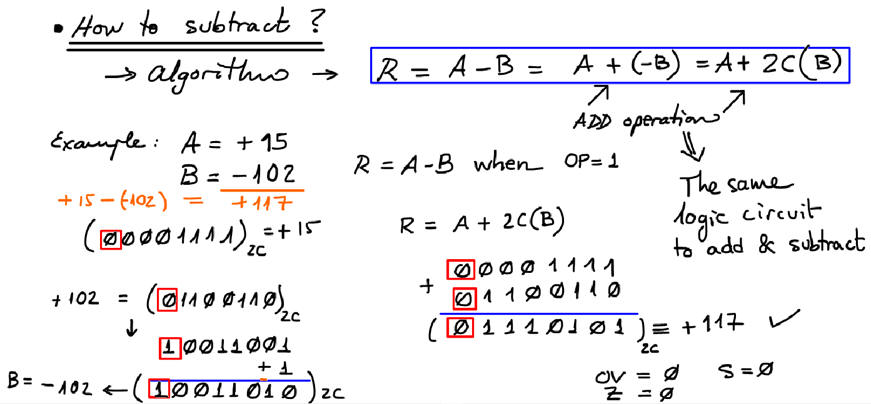
Subtraction

Example of subtraction

Play with the 8-bit 2C adder and subtractor Int_add_subt_8bit.pdsprj available in Proteus.

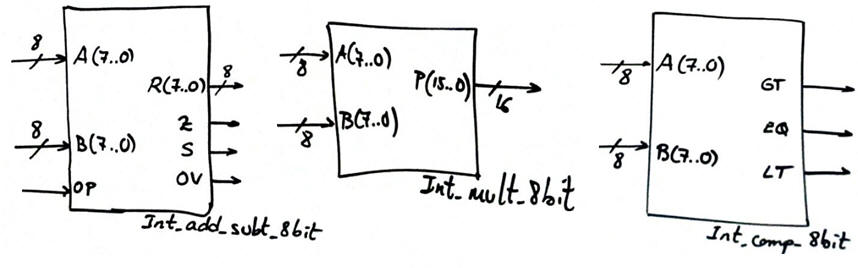
1.10.2. Adder-subtractor (Int_Add_Subt_8bit, etc.)

Int_Add_Subt_8bit

Ideas on planning the circuit. The first idea that comes in mind is selecting (using a MUX) the outputs from two operators that work in parallel generating both operations concurrently. An Octuple_MUX_2 device functionality is visualised in the picture.

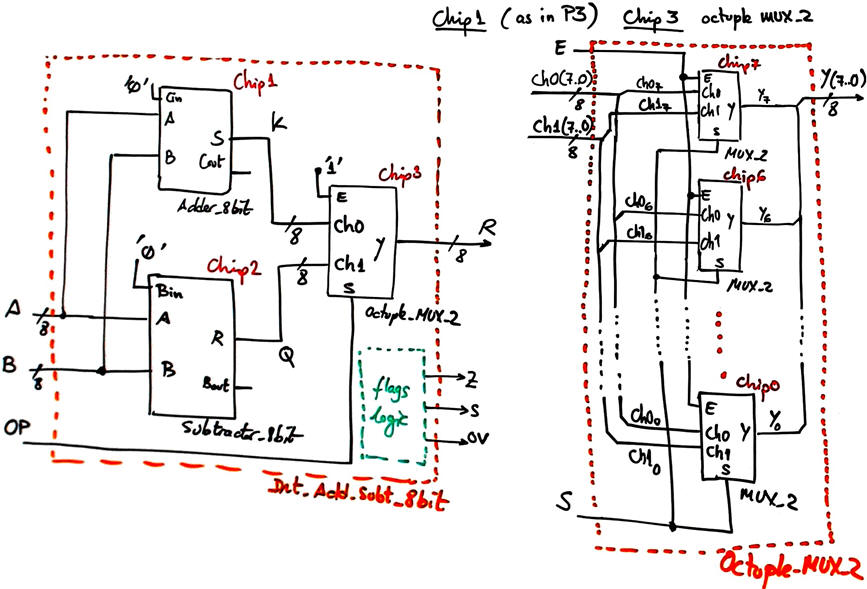
Int_Add_subt_8bit

Substractors can be inferred from specialised circuitry (see D1.13) or taking advantage of two's complement convention.

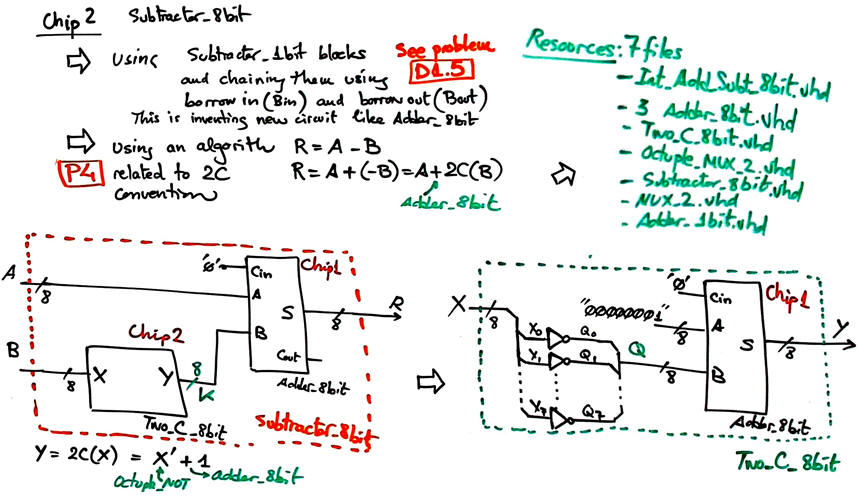
 Substractor_8bit

However, instead of implementing the circuit above, this time we can easily optimise the architecture using only one Adder_8bit, as developed in detail in Int_Add_Subt_8bit circuit. Further details on how to calculate flags are also explained.

 

1.10.3. Multiplier (Selectable_ Mult_8bit)

How to design a multiplier for integer numbers using radix-2 multipliers?

This is an example of an structural hierarchical 8-bit selectable multiplier Selectable_mult_8bit.pdsprj built in Proteus using our unsigned Mult_8bit from P3 and other blocks to organise the sign algorithm for integer numbers. The circuit inlcudes an input N that allows the selection of data to be radix 2 or integer (in 2C).

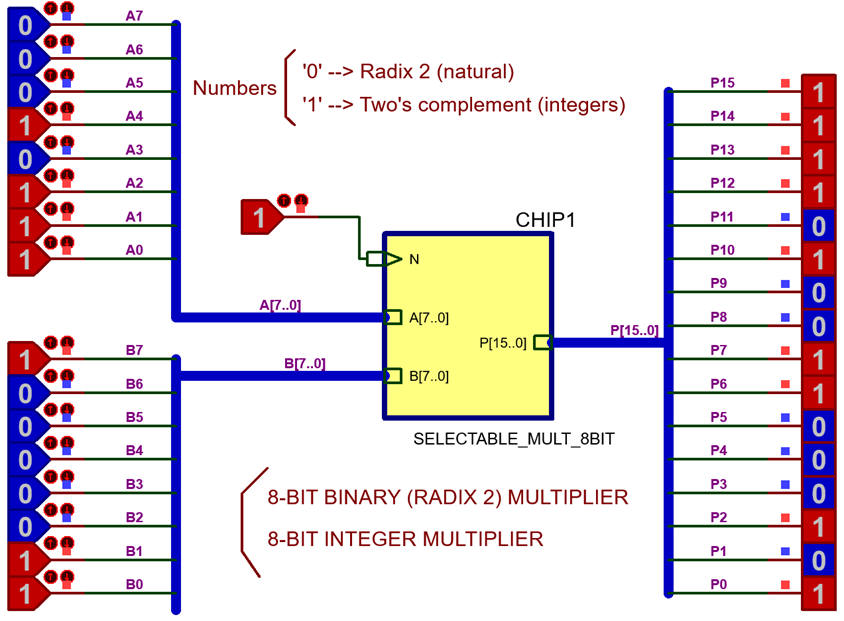
Selectablle Multiplier

This problem is interesting because puts at the limits our hierarchical multiple-file plan (at this introductory level that does not include generic VHDL statement). The networks of components is too complex to be described in a text file. Optional hint: if this problem has to be solved in VHDL using EDA tools, perhaps is better to describe the Mult_8bit using a behavioural approach plan B instead of this complicated plan C2 architecture. 

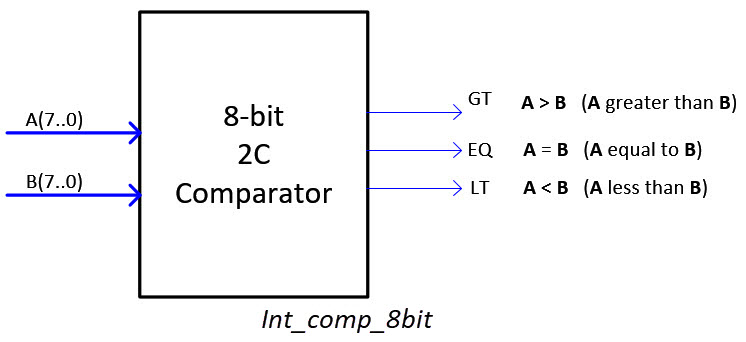
1.10.4. Comparator (Int_Comp_8_bit, etc.)

How to design a comparator for integer numbers using radix-2 comparators?. The idea is explored at D1.12.

Other basic operations in 2C: Comparison. The circuit Int_comp_8bit has to include 3 outputs: GT (greater than) to detect when A > B, EQ (equal to) to detect when A = B, and LT (less than) to detect when A < B.

int_comp_8bit

 

Exercise: solve these integer operations in binary 2C using an Int_add_subt_10bit chip (modify the size of the Int_Add_Subt_8bit planned in the hightlighted project (Fig. 5): 

(-201) + (-406)

(-201) - (-406)

Determine the result R(9..0) and the Z, N, OV flags. Check your answers using the computer calculator in programming mode.