UPC EETAC Bachelor's Degree in Telecommunications Systems and in Network Engineering EEL

 

Circuits based on logic gates

P1

Circuit_Q design

1. Analysis especifications

Deduce Circuit_Q truth table using method I (Boole's algebra). Check results analysing the same Circuit_Q using method II based on Proteus simulations.

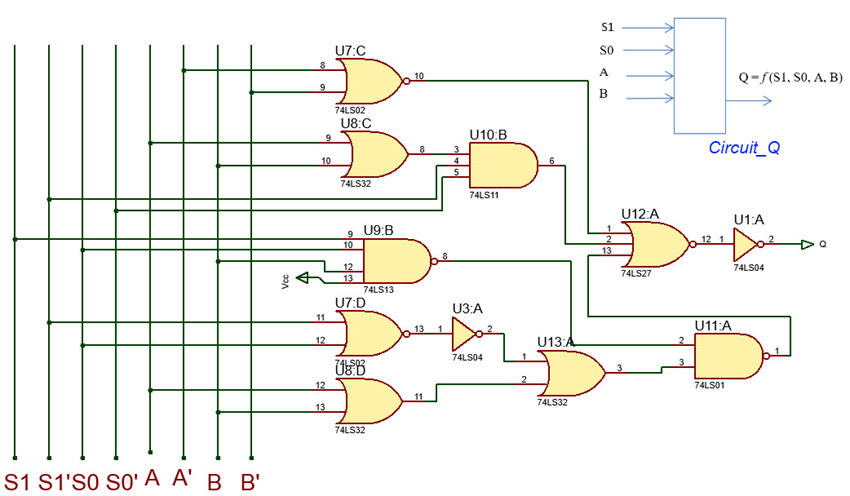Circuit_Q
Fig. 1. Circuit_Q based on logic gates.

 

2. Planning the analysis

Analysing Circuit_Q means deducing how it works for every input binary combination represented by its truth table. Fig. 2 shows methods I and method II on how to do it.

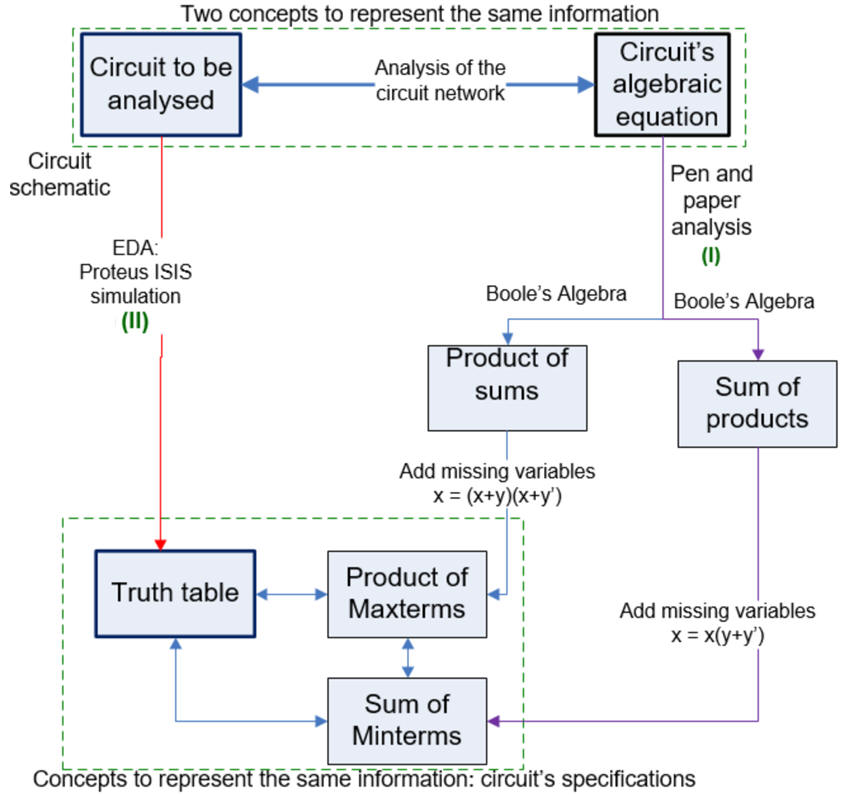Plan for solvin Circuit_Q
Fig. 2. Concep map for solving Circuit_Q.

1. To proceed with method I deduce the circuit's equation and apply Boole's algebra to get firstly the SoP or the PoS and secondly, the sum of minterns or product of maxterms, which are conceptually the truth table itself.

2. To test the truth table using method II capture the circuit in Proteus and run simulations.

 

3. Developing the analysis project

Analysis. Each analysis will be developed using the necessary tools. For instance:

 Method I: apply Boolean algebra to deduce the truth table and its minterms or maxterms.

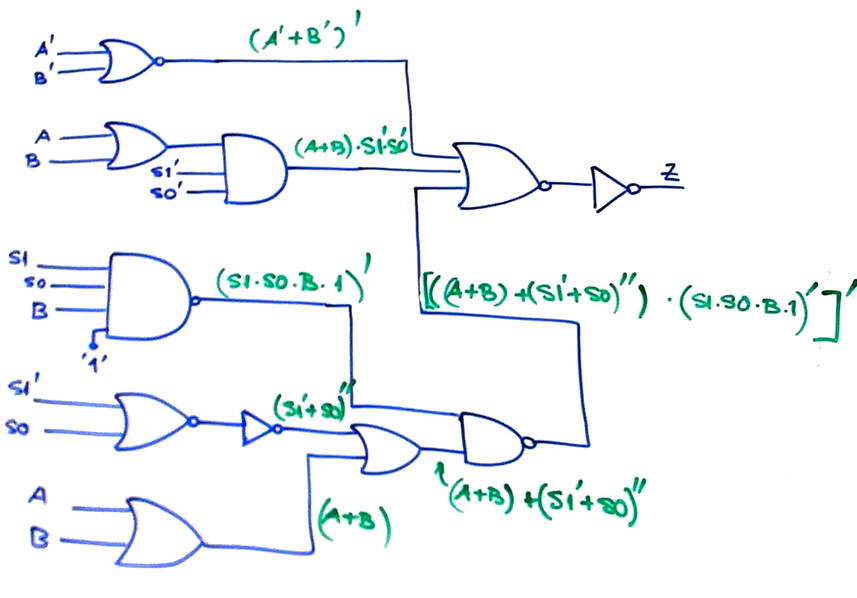Circuit analysis
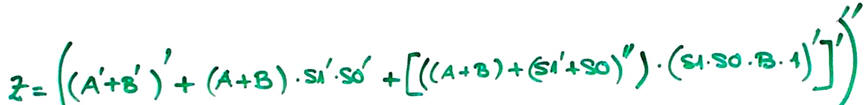Circuit_Q equation
Fig. 3. Circuit's algebraic equation.

From the initial circuit equation in Fig. 3 and the simplification process using Boole's algebra, we deduce the circuit's truth table in Fig. 4.


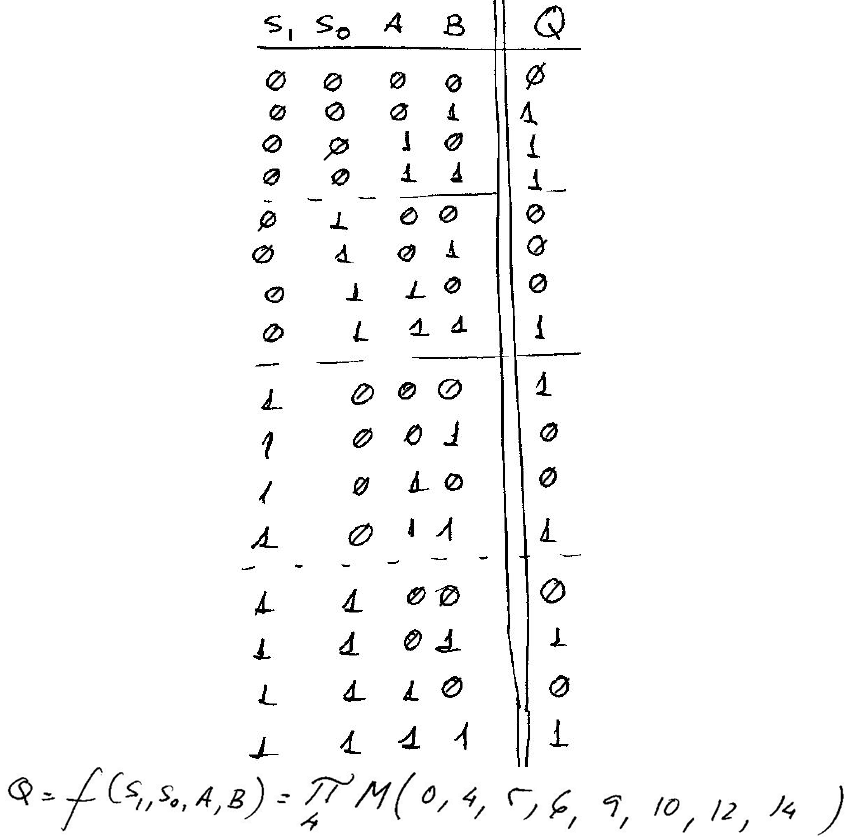Truth table
Fig. 4. Circuit_Q truth table.

 

4. Testing and validating analysis results

Method II: Draw Circuit_Q.pdsprj in Proteus using 74LS technology and run all input stimulus.

Simulation
Fig. 5. Simulating Circuit_Q in Proteus.

This is yet another way to verify Circuit_Q using method IV WolframAlpha equation.

 

5. Reporting the analysis

Using pictures, diagrames, sketches, handwritting discussions, etc.