UPC EETAC Bachelor's Degree in Telecommunications Systems and in Network Engineering EEL

Chapter 1 problems

      - A1.6 -

Analysing Circuit_G

Problems

A1.5

A1.7

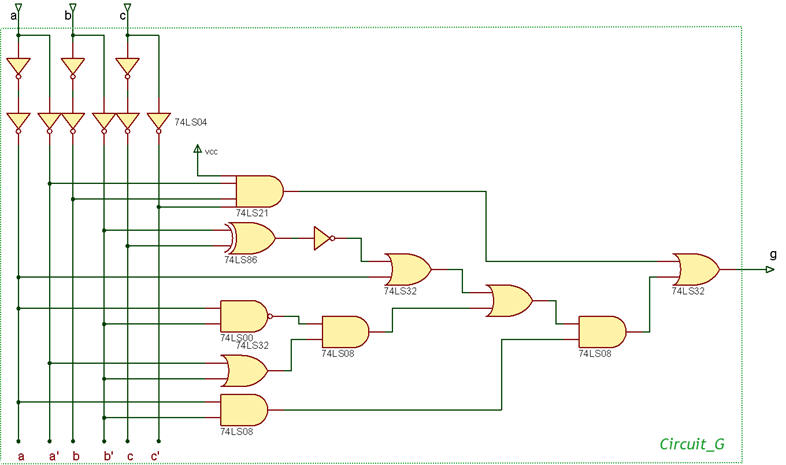
Using our analysis method I in CSD (L1.3) (Boolean algebra) find the circuit's symbol and truth table of the algebraic expression represented in Fig. 1. Name it as Circuit_G. Express the output as a sum of minterms and as a product of maxterms.

Circuit_G

Fig. 1. Combinational circuit g = f(a, b, c).

Deduce the circuit algebraic equation.

Transform the algebraic expression to SoP (or PoS) using Boole algebra.

Transform SoP (or PoS) to a sum of minterms (or a product of maxterms). Draw the truth table.

Draw a timing diagram considering all binary combinations and constant Min_Pulse = 2.3 μs.

Project location to save your paper solution, class notes, pictures, theory, etc.:

C:\CSD\P1\Circuit_G\algebra\(files)

Verify your results solving the same project using another analysis method.

Using our analysis method II (Proteus, electronic circuit simulations) find the circuit's symbol and truth table of the algebraic expression represented in Fig. 1. Project locations to save the complementary project for checking results:

C:\CSD\P1\Circuit_G\proteus\(files)

Proteus components library options:

 option #1.: LS-TTL

 option #2.: CMOS

Verify your results solving the same project using another analysis method.

Using our analysis method III (VHDL EDA synthesis and simulation tools) find the circuit's symbol and truth table of the algebraic expression represented in Fig. 1. Project locations to save the complementary project for checking results:

C:\CSD\P1\Circuit_G\VHDL\(files)

Target chip options:

 option #1.: MAX II

 option #2.: MAX 10

 option #3.: Cyclone IV

Verify your results solving the same project using another analysis method.

Using our analysis method IV (WolframAlpha, computer numerical engine) find the circuit's symbol and truth table of the algebraic expression represented in Fig. 1. Project locations to save the complementary project for checking results:

C:\CSD\P1\Circuit_G\wolfram\(files)

Verify your results solving the same project using another analysis method.