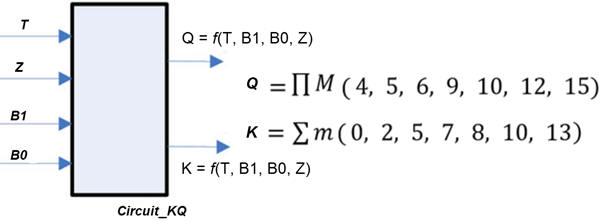UPC EETAC Bachelor's Degree in Telecommunications Systems and in Network Engineering EEL

L3.2

Lecture 3

L3.3: Designing logic functions using plan C2: MoD, MoM  

[P3] Method of decoders (MoD) and method of multiplexers (MoM).

L4.1

[4/10]

1.5.2.4. Plan C2: hierarchical design multiple-file (components and signals) 

Since now we have studied several strategies to implement logic functions based on canonical equations (maxterms or minterms), minimised equations (SoP or PoS), only-NOR or only-NAND transformations, or even any combination of equations. All of them related to a given circuit structure or plan A. Other methods are related to plan B: capturing the truth table or interpreting it as a flowchart.

1.5.2.4.2. Method of decoders (MoD)

Now, we will implement logic circuits using hierarchical structures plan C2 based on decoder components. Decoders are standard logic components explained in L2.3 the properties of which makes simple the implementation of logic functions.

How does the method of decoders for implementing logic functions work? 

 Example design: Circuit_C using MoD.

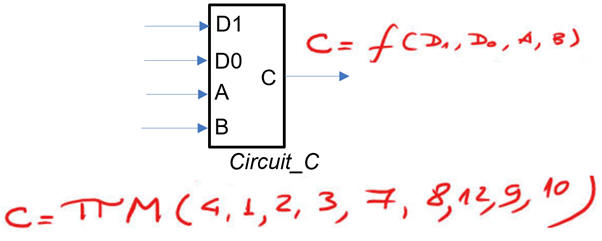Circuit_C

Fig. 7. Circuit_C symbol and truth table.

Hierarchical structure Circuit_C:

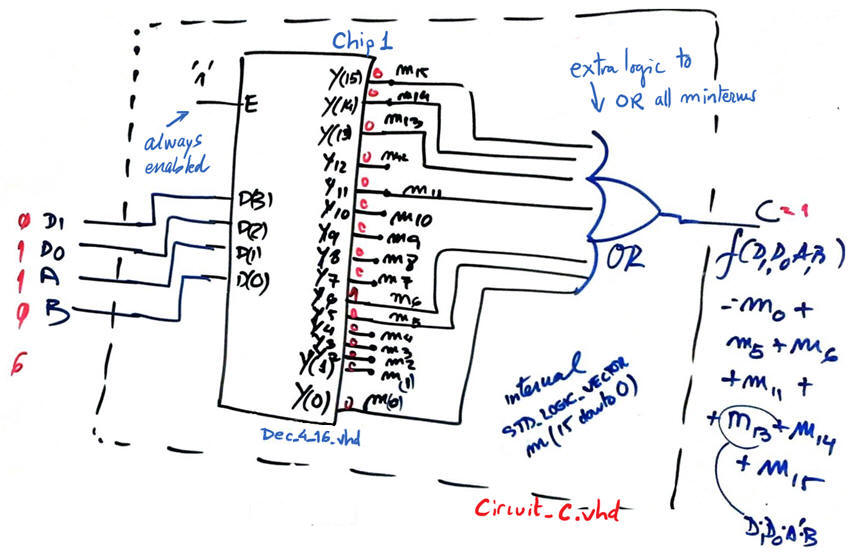Circuit_C architecture using plan C2

Fig. 8. Circuit_C hierarchical structure using a decoder component.

 

Example design: Circuit_K using the MoD.

 

Example design: 1-bit full adder (Adder_1bit) using MoD.

 

1.5.2.4.3. Method of multiplexers  (MoM)

Multiplexers are standard logic components explained in L2.1.  How does  the method of multiplexers for implementing logic functions work?

A) Draw the symbol and expand the truth table to show all combinations

B) Section the truth table accordingly to the number of MUX channels

C) Connect the selection inputs to circuit inputs assigning inputs from from left to right.

D) Solve the remaining combinational logic that has to be attached to each channel

Example design: Comb_circuit using MoM and MUX_8, MUX_4 and MUX_2.

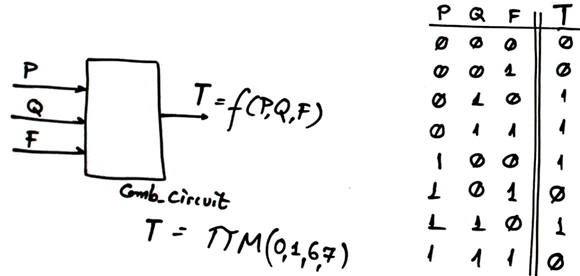Example function

Fig. 9. Comb_circuit symbol and truth table.

Fig 10 shows the solution when designing the Comb_circuit uisng the MoM and a MUX_8.

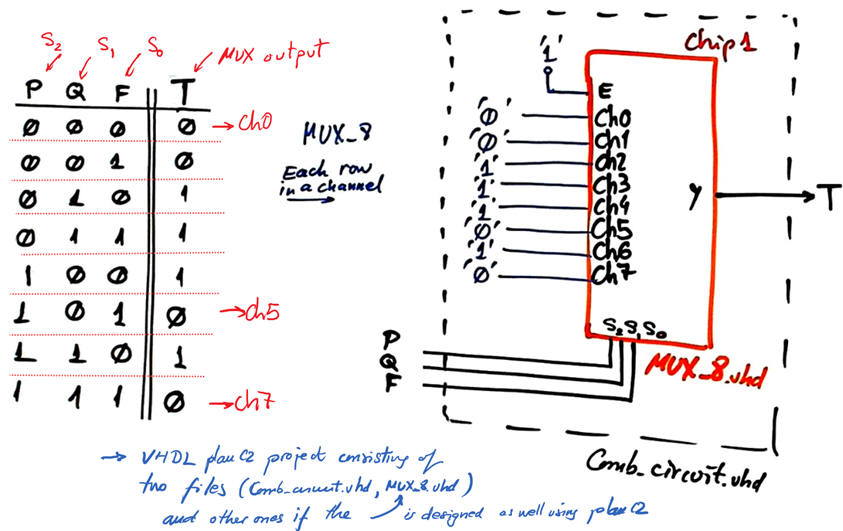MoM using a MUX_8

Fig. 10. Comb_circuit using MoM and a MUX_8.

Fig 11 shows the solution when designing Comb_circuit using MoM and a MUX_4.

Comb_circuit using MoM and a MUX_4

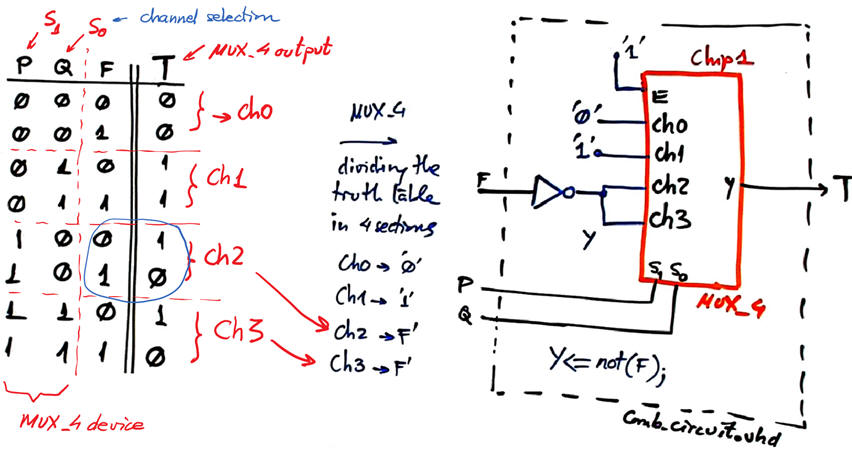Fig. 11. Comb_circuit using MoM and a MUX_4.

Fig 12 shows the solution when designing Comb_circuit using MoM and a MUX_2.

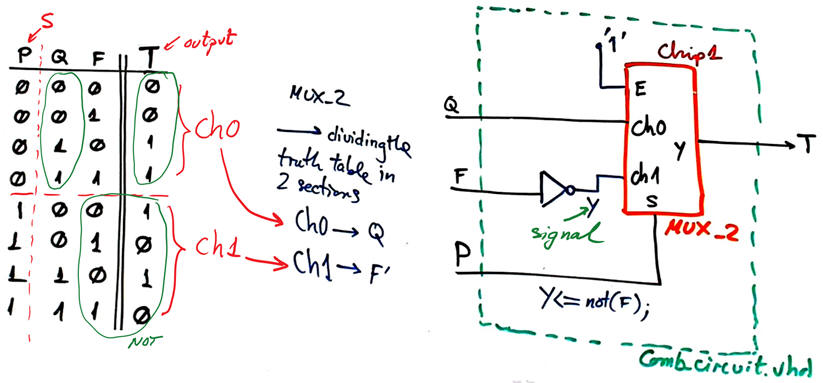Com_circuit using MUX_2

Fig. 12. Comb_circuit using MoM and a MUX_2.

A good idea now is to translate to VHDL the schematics in Fig. 10 (Comb_circuit.vhd), Fig. 11  (Comb_circuit.vhd) and Fig 12  (Comb_circuit.vhd), and run synthesis and simulation  (Comb_circuit_tb.vhd) to check whether the circuits generates the truth table in Fig. 9. As usual, place each project in a different folder:

- C:\CSD\P3\Comb_circuit_MoM_MUX_8\(files)

- C:\CSD\P3\Comb_circuit_MoM_MUX_4\(files)

- C:\CSD\P3\Comb_circuit_MoM_MUX_2\(files)

 

Example design: 3-bit even parity generator using MoM and a MUX_2.

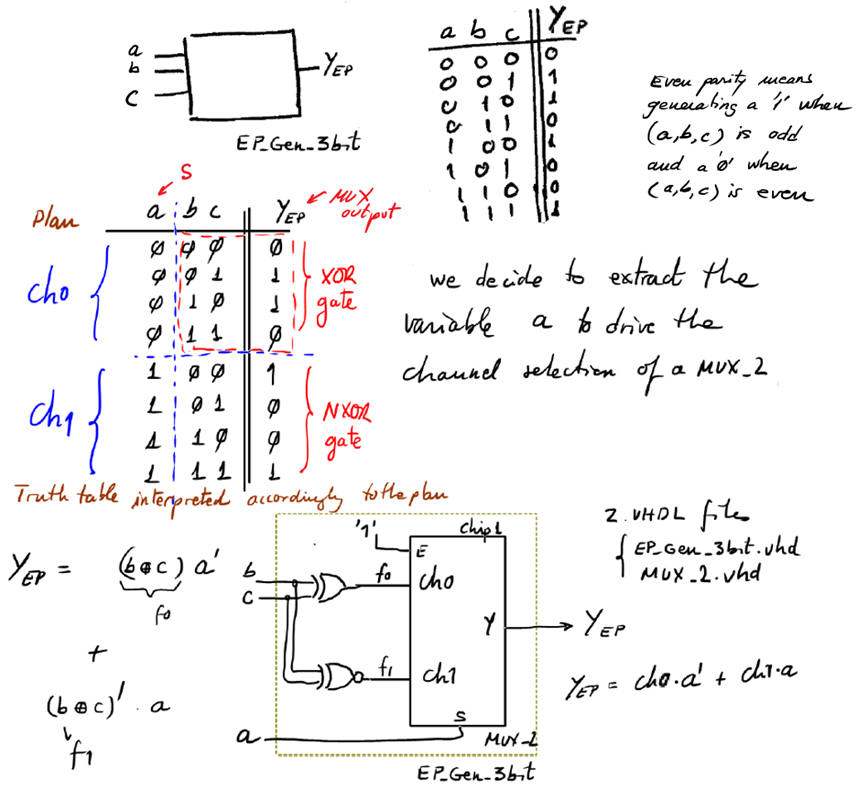Discussion on even parity

Fig. 13. Discussion on how to implement the 3-bit even parity generator using MoM and a MUX_4.

 

Example design: Circuit_C using MoM and a MUX_4.

Circuit_C

Fig. 13. Circuit_C symbol and truth table.

A solution using MoM and MUX_4 is represented in Fig. 14.

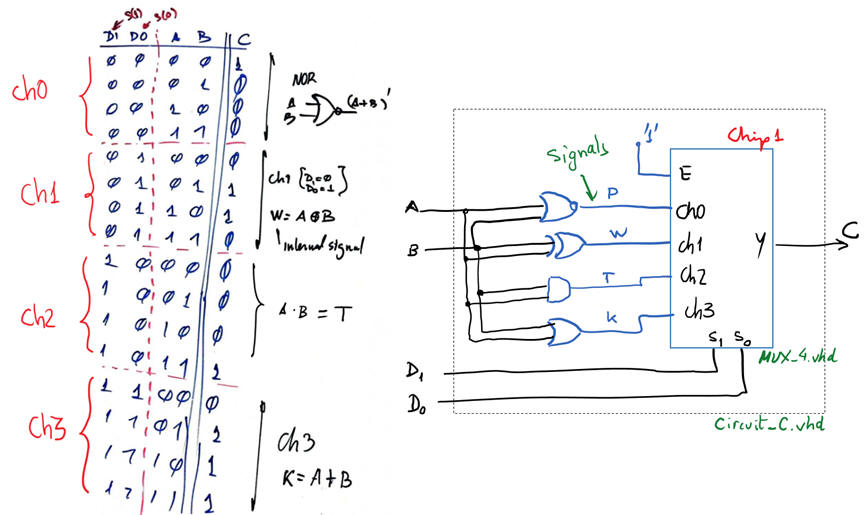Circuit_C

Fig. 14. Proposed solution for Circuit_C

 

Example design:

- Comp_1bit using MoM and MUX_2 (GT), MUX_4 (EQ) and MUX_8 (LT)

Example design:

- 1bit_adder based on the MoM using MUX_2 for So and MUX_4 for Co. Lab3.

 

Exercise: Design the Circuit_KQ using plan C2 and these two alternative hierarchical architectures:

- MoD

- MoM and a MUX_4 for Q and a MUX_2 for K.

Circuit_KQ