|
L1.4: Designing combinational circuits P1 design plan A: canonical circuits, minimisation (minilog), circuits using SoP, PoS |
[12/9] |
1.5. Design flow for inventing combinational circuits using VHDL
1.5.1. Specifications, design concept map
1.5.1.1. Symbol or entity
1.5.1.2. Truth table
1.5.1.3. Example timing diagram
The main concepts related to our circuit consist of: symbol, truth table, timing diagram applying some values, and a bit of theory or context.
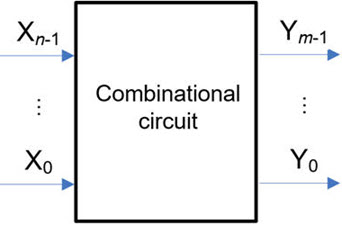 |
Fig. 1. Symbol (entity) of a generalised combinational circuit. In CSD we propose up to fourteen architecture variations for inventing logic functions using VHDL or programming languages. |
1.5.2. CSD design plans
| Strategies for designing
combinational circuits |
Plan A: structural, equation-based translation to VHDL in a single file (flat design)General ideas on designing combinational circuits using networks of logic gates covered in P1. 1) Canonical equations: sum of minterms. The truth table equation. 2) Canonical equations: product of maxterms. The truth table equation. 3) Minimised equations: SoP, the output from minilog.exe. Used in sPLD-CPLD macrocells. 4) Minimised equations: PoS, minilog.exe output results. 5) Modified equations to use only-NOR logic gates (universal gate). 6) Modified equations to use only-NAND logic gates (universal gate). 7) Mixing equations of any kind.
Plan B: behavioural, direct truth table/algorithm translation to VHDL in a single file (flat design)Covered from P2 where we start classifying standard logic circuits. 8) Translating the truth table directly to VHDL or to an algorithm represented by a flowchart.
Covered in P9 as an easy way to introduce microcontroller programming in C and basic I/O. 9) Translating the truth table directly to C language (or Python) as software to be executed in a microcontroller.
Plan C1: hierarchical structure of components (flat design, single-file)10) Not practical, and not used in CSD Chapter 1. Indeed, we use it only for describing FSM architecture in Chapter 2.
Plan C2: hierarchical structure of components, multiple-file designCovered in P3) where large and chained circuits are explained: 11) The method of decoders (MoD) 12) The method of multiplexers (MoM) 13) Circuit expansion. Most of circuits that deal with n-size vectors can be organised using identical chips or similar ones chained by means of a given pattern (i.e. carry in, carry out; enable in , enable out) using special inputs and outputs. For instance, we can invent an Enc_4_10 using Enc_2_4. Covered in L5.4 were memory components are introduced: 14) The method of ROM/RAM memory chips or lookup tables (FPGA - LUT) |
1.5.2.1. VHDL plan A: structural/equations single-file
1.5.2.1.1. Canonical equations: sum of minterms or product of maxterms.
Wikipedia entry for canonical forms. For example, we can invent four circuits from Circuit_W truth table as shown in Fig. 2:
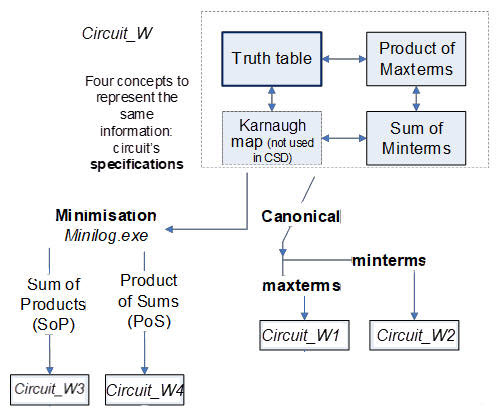 |
Fig. 2. Circuits W1 and W2 from the canonical equations, and circuits W3 and W4 from minimised equations. |
Project 1: Specifications: Invent Circuit_W1 from the truth table of Circuit_W using the canonical expression product of maxterms.
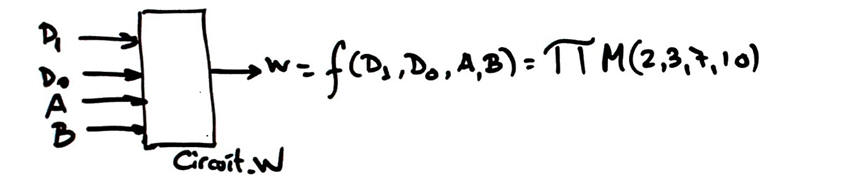 |
Fig. 1. Symbol and truth table as a product of maxterns. |
Plan and development:
Location for this project files, for instance: pictures, scanned files, report, etc. at:
C:\CSD\P1\Circuit_W\Circuit_W1\
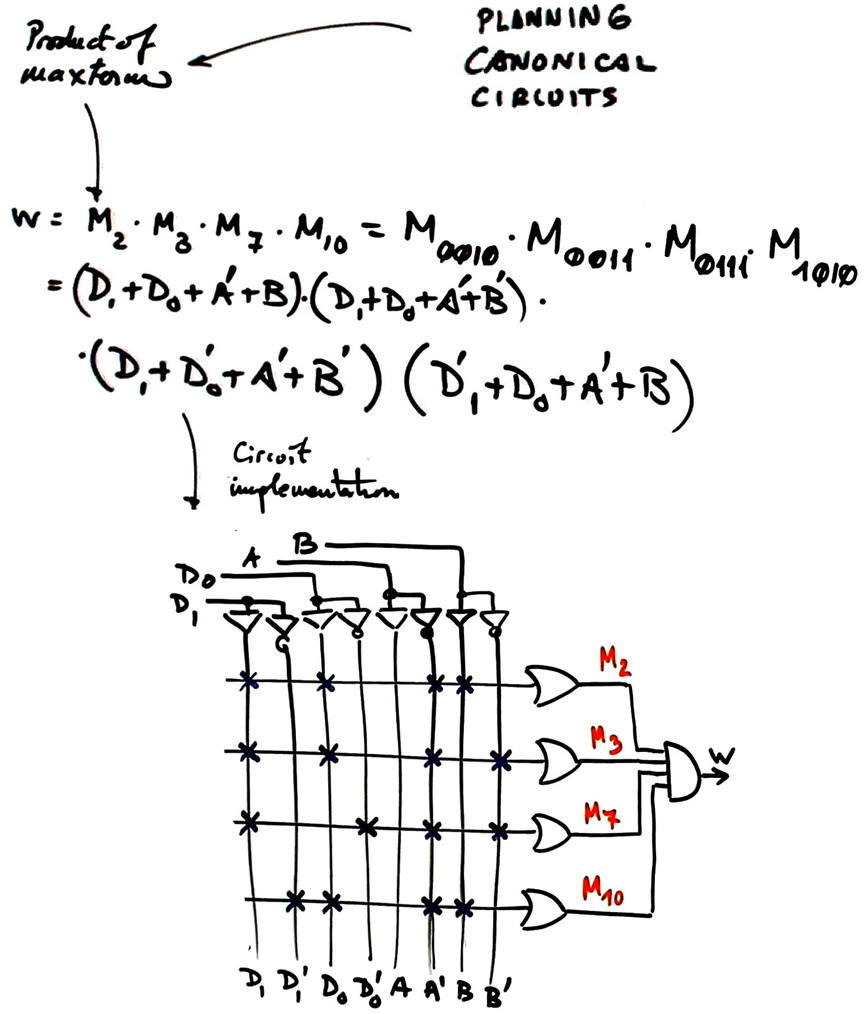 |
Fig. 2. Immediate circuit representing the product of all maxterms. |
Test: if you test the circuit for example using WolframAlpha or Proteus you will place in the project folder your computer files such as "equations_W.txt" or "Circuit_W.pdsprj". In this case, checking is simply verifying the truth table.
Project 2: Specifications: Invent Circuit_W2 from the truth table of Circuit_W using the canonical expression sum of minterms.
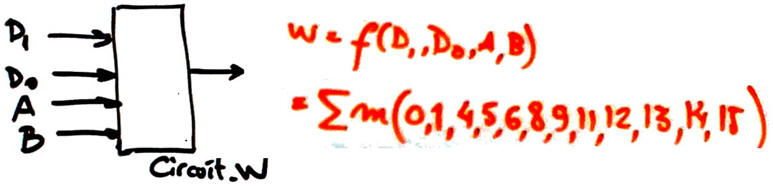 |
Fig. 1. Symbol and truth table as a sum of minterms. |
Plan and development:
Location for this project files, for instance: pictures, scanned files, report, etc.
C:\CSD\P1\Circuit_W\Circuit_W2\
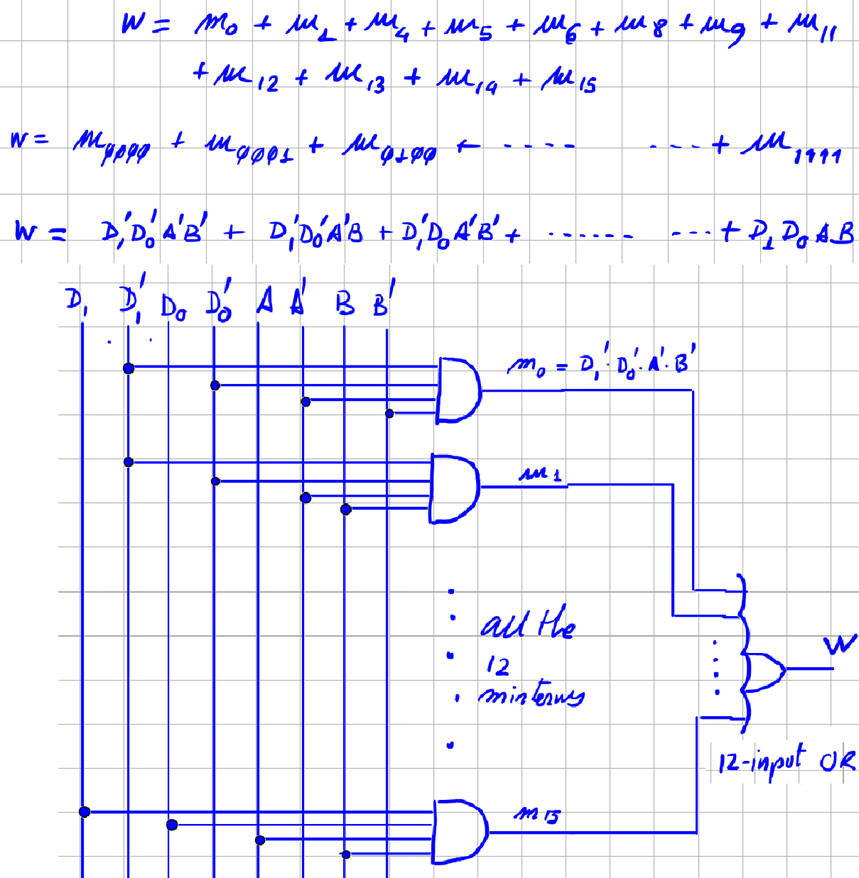 |
Fig. 2. Immediate Circuit_W2 representing the sum of all minterms. |
Test: if you test the circuit for example using WolframAlpha or Proteus you will place in the project folder your computer files such as "equations_W.txt" or "Circuit_W.pdsprj". However, in this case:

1.5.2.1.2. Minimised equations: SoP or PoS
- Espresso heuristic algorithm: minilog.exe (we use Notepad++ as enriched text editor for writing text tables).
- Truth table translated to Minilog text input format (.tbl)
- Minilog minimisation results: SoP or PoS logic equations and equation converter
For example:
Project 3: Specifications: Invent Circuit_W3 from the truth table of Circuit_W using minimised SoP
Plan: this is the procedure to obtain results and complete the project:
1. Circuit_W3 project location:
C:\CSD\P1\Circuit_W\Circuit_W3\(files)
2. Find and modify a similar tbl file, fr example you can use the file Circuit_P.tbl in minilog tutorial and rename and adapt it to: Circuit_W.tbl
3. Run Minilog and simplify using single output mode (SoM), equation output format, and choose SoP.
4. Equation format that has to be reprocessed by equation_converter.exe so that you get SoP equation with the project entity names for inputs and outputs.
5. Draw the circuit.
6. Check the circuit's equation using WolframAlpha or Proteus.
Development:
- Minilog file describing the truth table: Circuit_W.tbl

Test: This means verifying that the circuit that you have designed has the given initial truth table. For instance, this is the Proteus capture: Circuit_W.pdsprj.
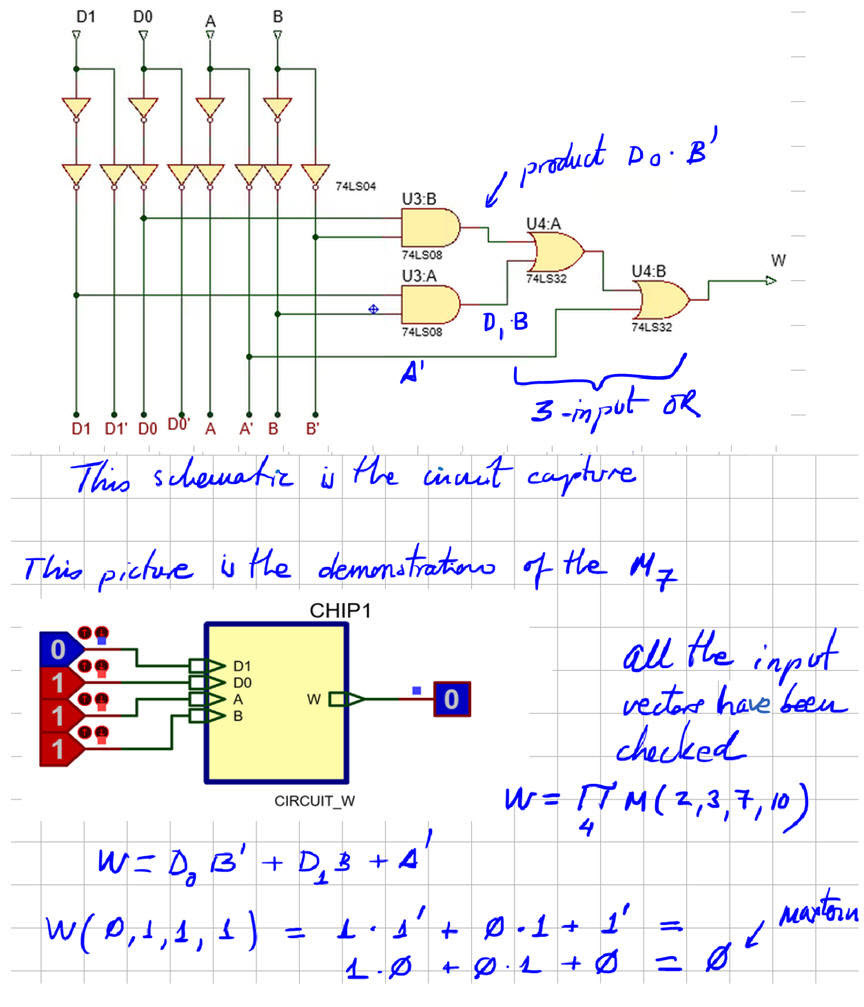
Exercise: Specifications: Invent Circuit_W4 from the truth table of Circuit_W using minimised PoS
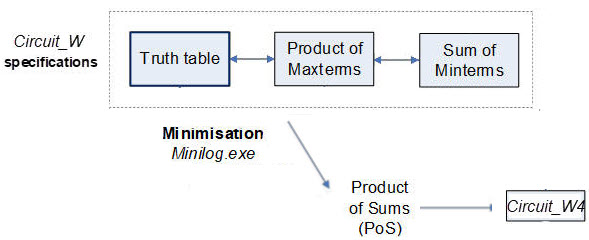 |
Fig. 1. Circuit_W4 infrred from the minimised PoS. |
Plan: Circuit_W4 project location: C:\CSD\P1\Circuit_W\Circuit_W4\(files)
- Run Minilog and simplify using single output mode (SoM), equation output format, and choose PoS.
Development. Draw the logic circuit
Test: Use Proteus to check the truth table of this circuit or compare your results with your team mates.


