UPC EETAC Bachelor's Degree in Telecommunications Systems and in Network Engineering EEL

Chapter 1 problems

     - D1.13 -

8-bit subtractor using Subtractor_1bit

Products

D1.12

D1.14

1. Specifications

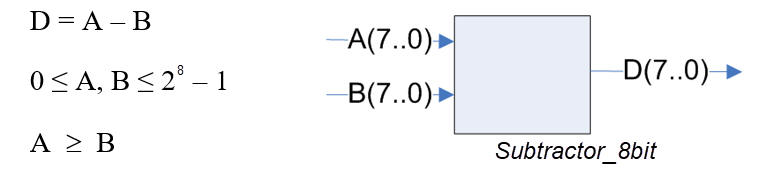
We want to implement a circuit for subtracting 8-bit binary radix-2 numbers as represented in Fig. 1. 

The same project B3.13 is proposed in Chapter 3 for learning the basics of μC software organisation and basic digital I/O.

Subtractor symbol

Fig. 1. The entity of a Subtractor_8bit and the operands range.

The strategy is to use plan C2, chaining 1-bit subtractors instead of the standard way based on 1-bit adders and two's complement convention discussed in P4. Thus, the circuit will work only with radix-2 numbers. Fig. 2 shows the building block Substractor_1bit.

Symbol of the Subtractor 1bit

Truth table

Fig. 2. The entity of a Subtractor_1bit and its truth table.

So, we can chain many Subtractors_1bit by connecting the "borrows" in the same way we connect the "carry" when adding:

Algorithm

Fig. 3. Algorithm for a chained 8-bit subtraction.

Some questions:

- Try at least three operations:

A = 230, B = 45; A = 187, B = 177; A = 177, B = 187

- Draw a sketch of a timing diagram.

 

2. Planning

Conceiving the Subtractor_1bit component:

Option plan A: Implement the Subtractor_1bit using only NAND2 gates.

Some notes on its solution.

Option plan B: Write the code for the Subtractor_1bit in VHDL using a behavioural approach.

Conceiving the Subtractor_8bit: 

Plan C2:

Draw the schematic of the 8-bit ripple subtractor (Subtractor_8bit) and describe it in VHDL, using components.

 Implement the logic circuit of a pair of flags or indicators to detect special events like:

- A zero result D = A - B = 0

- A negative number D < 0 (A<B) 

 Develop the circuit targeting an Intel FPGA MAX II and inspect the RTL and the technology view.

 Test your circuit writing a VHDL simulation testbench from the timing diagram in the specifications.

This is the former CSD problem collection.