UPC EETAC Bachelor's Degree in Telecommunications Systems and in Network Engineering EEL

L2.5

Lecture 1

L3.1: Arithmetics in radix-2

[P3] Binary codes and radix-2 adders, comparators and  multipliers

L3.2

[1/10]

1.8. Binary codes and code converters

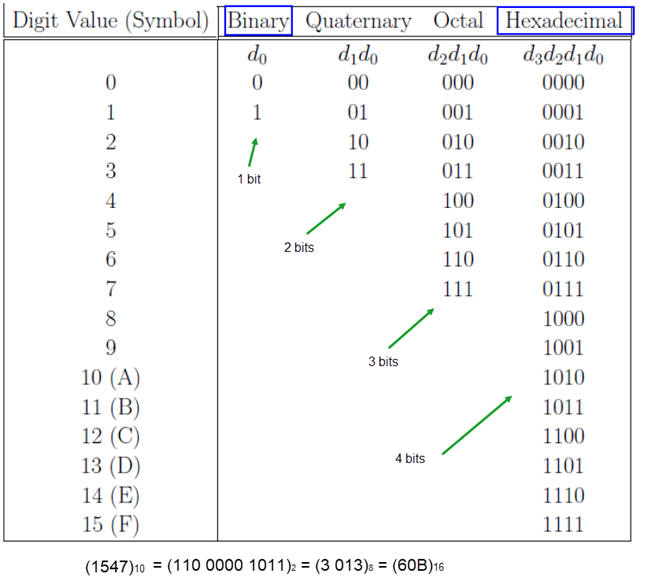
1.8.1. Number systems. Binary radix 2 (base 2), octal (base 8, hexadecimal (base 16)

number system

Radix-2

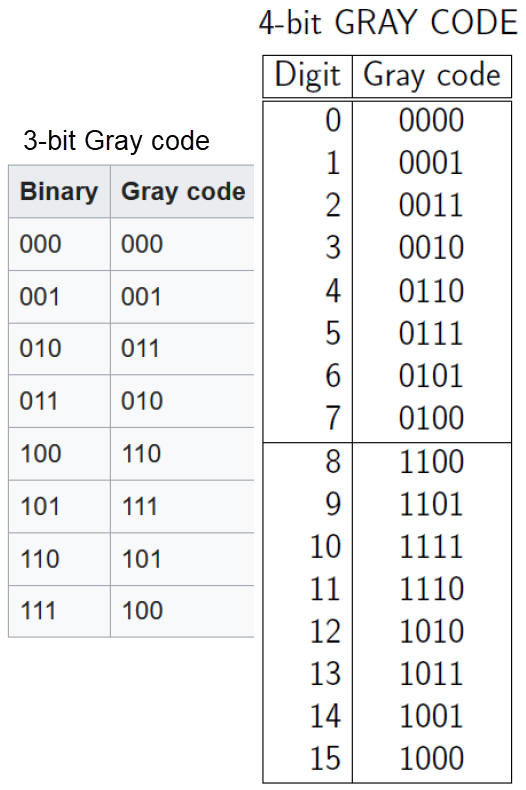
1.8.2. Gray code

Gray 

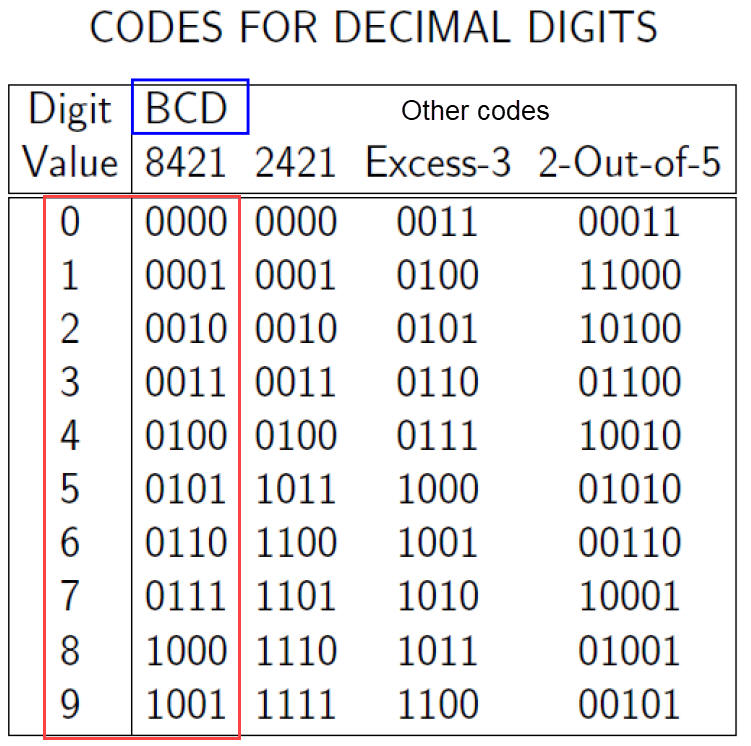
1.8.3. BCD (binary-coded decimal)

BCD 

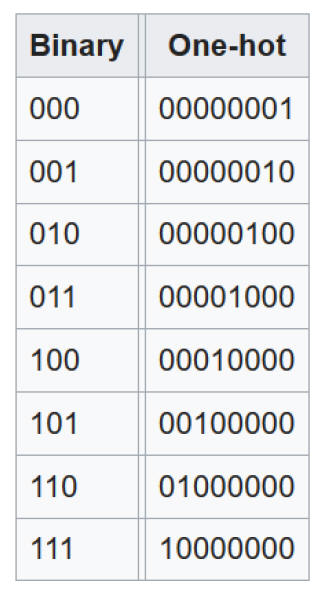
1.8.4. One-hot and one-cold

onehot

1.8.5. Johnson

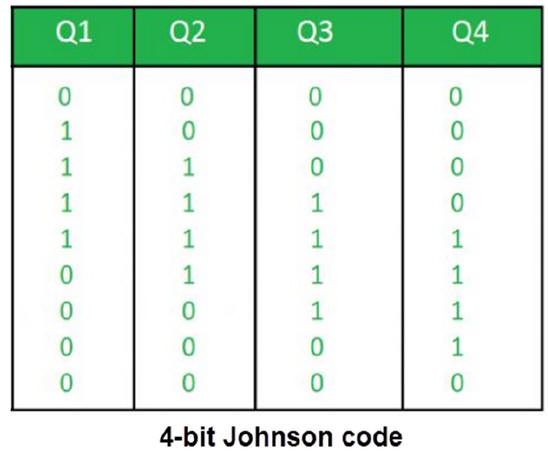
Johnson

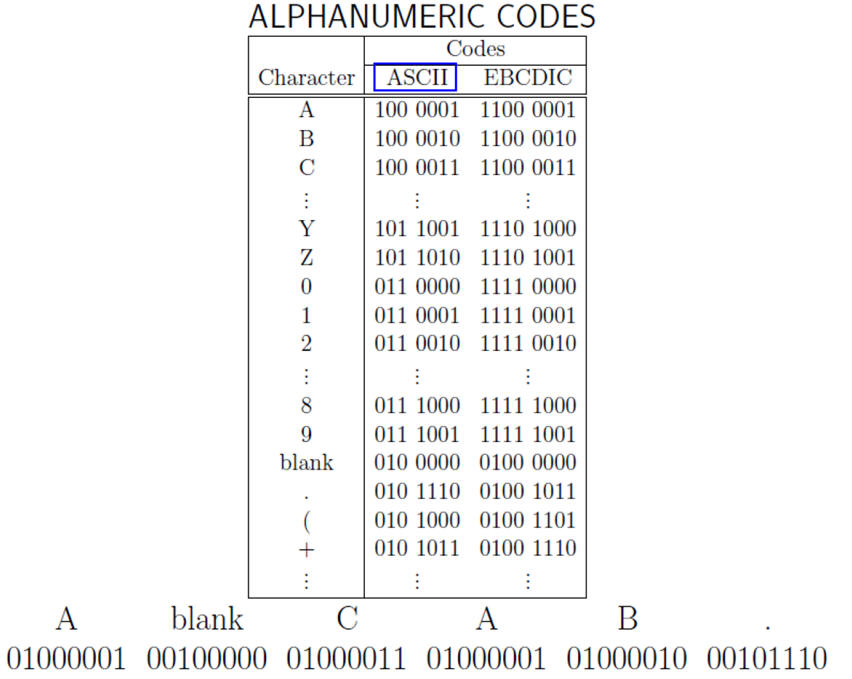
1.8.6. Keyboard symbols: ASCII, etc.

ASCII

1.8.7. MORSE code. MORSE code translator.

1.8.8. Code converter circuits

1.8.8.1. Bin_BCD_converter_6bit

1.8.8.2. Gray_Bin_converter_4bit

1.9. Binary (radix-2, base-2) arithmetic circuits

1.9.1. Addition

1.9.1.1. 1-bit adder (Adder_1bit)

Binary numbers, symbols, range and how to perform additions.

Additions

Conversion from binary to decimal, decimal to binary. Hexadecimal numbers. How to use the computer calculator in programming mode to work with bin/hex/oct/dec numbers.

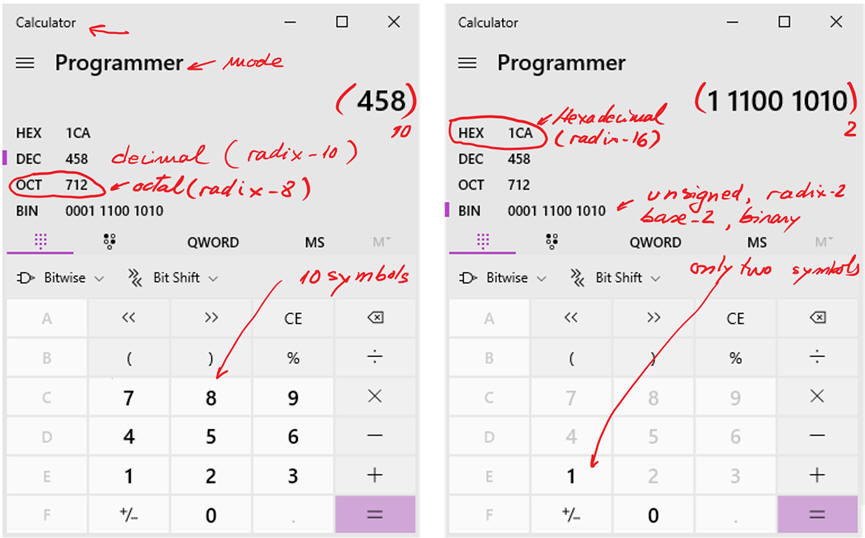
PC calculator in mode programmer

Planning 1-bit expandable adders: tutorials on how to design the 1-bit full adder using our plans:

- Plan A: structural (equations)  Adder_1bit

- Plan B: behavioural Adder_1bit

- Plan C2: Hierarchical multiple-file Adder_1bit

1.9.2. Comparator

1.9.2.1. Expandable 1-bit comparator (Comp_1bit)

Symbol and truth table.

Symbol Truth table

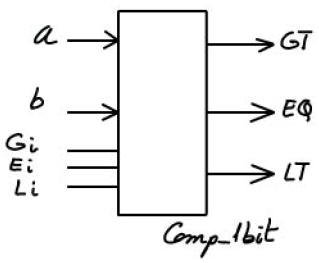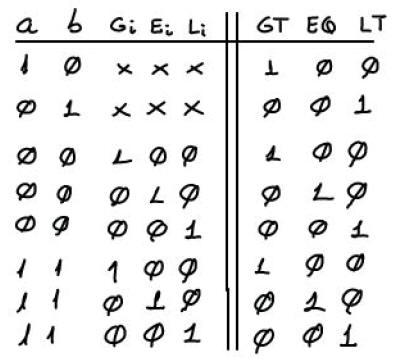Planning expandable comparators:

- Plan A: 1-bit expandable comparator Comp_1bit 

- Plan B: 1-bit expandable comparator Comp_1bit 

- Plan C2: 1-bit expandable comparator Comp_1bit using the MoM

 

1.9.3. Multiplier

1.9.3.1. 1-bit multiplier cell, Mult_1bit

 

 

Exercise: Convert the following numbers and charecters:

(345)10 = (        )2 = (          )BCD =  (      )16

 

10101)2 = (      )GRAY

 

10111)GRAY = (       )2 = (      )BCD

 

(1100001111010101010001001)2 = (        )16  = (          )BCD =  (       )10

 

(6BFA87)16 = (        )2 = (          )BCD =  (      )10

  

"Hello World 2024"  = (             )ASCII  = (             )MORSE