UPC EETAC Bachelor's Degree in Telecommunications Systems and in Network Engineering EEL

 

Filtering and synchronising inputs: push-button debouncer

P6
1. Specifications Planning Developing Testing  Prototyping

Let us design a digital filter to clean the noisy signal generated when pressing and releasing a mechanical key or pushbutton. When clicking and releasing a key, the electrical signal generates a random number of ones and zeros (signal bouncing) that must be filtered out in order to interface correctly a digital circuit. Additionally, the idea is to synchronise the key signal (an asynchronous input) to the system CLK, so that it can be correctly sampled. This phenomena is sampled correctly in the range of 100 Hz.

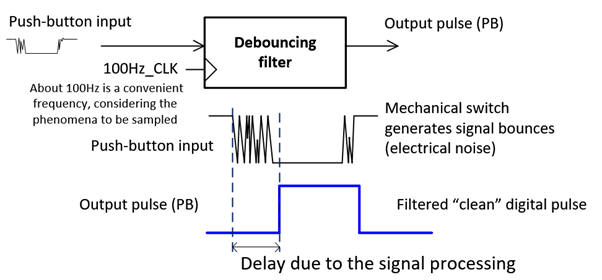Debouncing process

Fig. 1. Example of the waveforms describing the phenomena. Clicking a mechanical key has to generate a clean single pulse (visio).

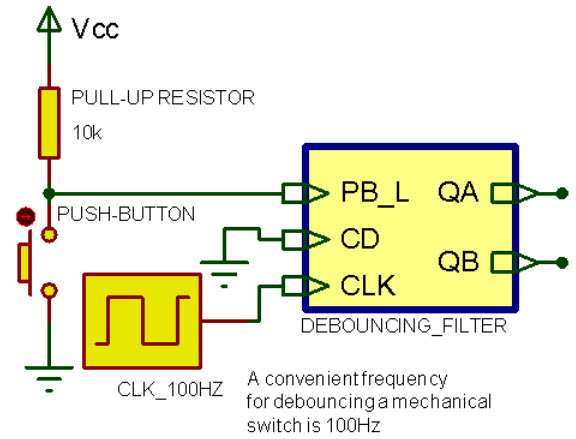
Thus, we aim to design the circuit in Fig. 2 using a FSM strategy and with this conditions:

- After clicking the push button (which is active low), the QA and QB will go high ('1') only after that 3 consecutive '0' have been sampled. This situations means that the signal is already stable with someone currently pressing the key.  QA will be assessed only for one clock pulse.

- Once the pushbutton is released, QB will go low after 2 consecutives '1' sampled. This means that duration of the QB pulse (for instance counting the number of CLK pulses while the signal is high) is a measurement of the time in which the key (or the sensor) is pressed (or active).

debouncer
wave

Fig. 2. The circuit to be designed have two outputs: QA to produce a single pulse, and QB to generate a pulse that last as long as the key is being pressed.

Before attempting the design of the debouncing filter, it is better to pay attention on (a) how an analogue filter may work as studied in the annex, (2) how the idea of sampling signals works for a simple key or push-button rec. The questions to solve are: what is the best sampling frequency? why it is necessary a FSM acting as a digital filter instead of a simpler D_FF for this function of conditioning or interfacing a push-button?

push-button

Fig. 3. This is the kind of signal generated when clicking and releasing a button.

 

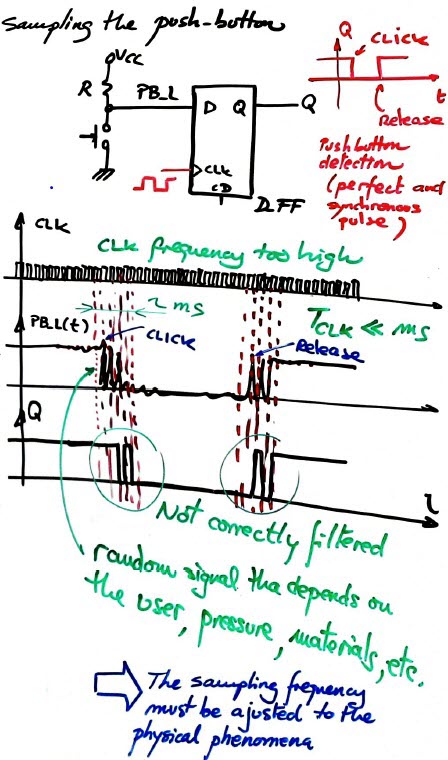push button sampling high frequency

Fig. 4. Sampling with a D_FF. A sampling frequency that is too high with respect to the physical phenomena of clicking and releasing a key will not filter the signal correctly. Signal bounces will be captured and thus, many (random) digital pulses will be generated every time that the key is clicked and released. 

 

too low sampling frequency

Fig. 5. Sampling with a D_FF. A sampling frequency that is too low with respect to the physical phenomena of clicking and releasing a key may not be able to detect the event.

Additional references:

- Christoffersen, J., "Switch bounce and how to deal with it", All about circuits, 2015.

- A reference from the MIT: Study of a level-to-pulse converter. Why to synchronise input signals?

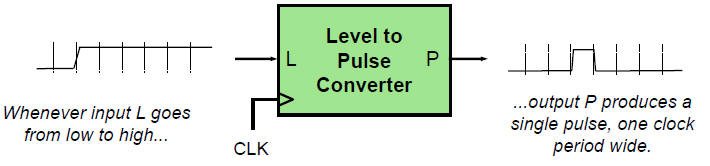level to pulse

Fig. 6. Detecting and synchronising an external event (rising edge) input.

 

Specs 2. Planning Development Testing Prototyping

Let's infer the state diagram so that the system is able to memorise the sequence of zeros and ones that will produce the outputs QA and QB.

State diagram
Fig. 7. Proposed state diagram.

Let's obtain the truth tables of the CC1 and CC2 combinational circuits, so that they can be easily translated to VHDL.

 

Specifications Planning 3. Development Testing Prototyping

This is the debouncing_filter.vhd VHDL code

Let's see if the synthesiser interprets correctly this FSM descriptions producing the RTL picture in Fig. 8.

picture
Fig. 8. The RTL schematic.

 

picture
Fig. 9. Number of registers used in the synthesis of the circuit.  

 

Specifications Planning Development 4. Testing Prototyping

This is a sample test bench file debouncing_filter_tb.vhd.

1) Functional simulation. Run the EDA VHDL tool and demonstrate how the circuit works adding comments to the printed sheet of paper containing the waveforms.

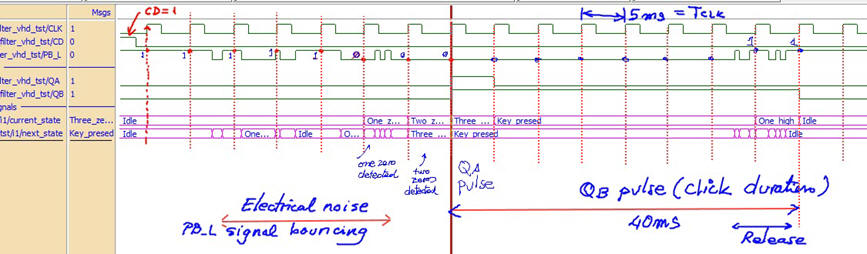debouncing functional waveform

Fig. 10. Example of a timing diagram to show how the circuit works.

 

Specifications Planning Development Testing 5. Prototyping

Use training boards and perform laboratory measurements to verify how the circuit works. The annex below shows experiments and results when trying to characterise an analogue filter.

 

6. Report

Project report starting with the template sheets of paper, scanned figures, file listings, docx , pptx, or any other resources.

 

Annex: Experimenting with push-buttons and analogue filtering.

We can easily observe and characterise typical push-button waveforms using logic analyser and oscilloscope instruments. Fig. 1 shows a basic set-up for an active-low push-button. We can also add a NOT gate to better obtain digital values and sharper edges.

Circuit and wafeforms expected

Fig. 1. Detecting and synchronising an external input.

Fig. 2 shows the circuit ready for experimentation in a protoboard. Let us try several capacitors.

Circuit in the laboratory

Fig. 2. The push-button experiment monitored by the VB8012 instrument

Fig. 3 shows the waveforms captured using C = 1.5 pF. Small value, as if it were not placed in the circuit, somewhat simulating all the parasitic capacitances of wires and instrument probes. Practically for all clicks several signal bounces are recorded in the event by the logic analyser when the signal is falling from high to low.  

1.5 pF waveforms

Fig. 3. Example click waveforms using C = 1.5 pF. t = R·C = 15 ns.

We can also represent, as in Fig. 4, the NOT gate input and output signals for the same C = 1.5 pF. Waveform shapes, event duration and bounces detected depends much on user click pressure on the button, and the quality and materials of the button itself.

Signals using NOT (C = 1.5 pF) (1)
Signals using NOT, C = 1.5 pF (2)

Fig. 4. Example click waveforms when using the NOT gate SN74LS04, C = 1.5 pF. For every click captured, signals are different, and generaly the NOT gate does a good job cleaning and sharpening the digital signal. NOT gate  propagation delay from low to high is tPLH = 10 ns. 

Higher capacitors generate ringing waveforms. Even if the signal is much filtered, we cannot get rid of signal bounces. 

Waveforms (10 nF)
Waveforms 10 nF, using NOT

Fig. 5. Example click waveforms using C = 10 nF. t = R·C = 100 ms. With and without the NOT gate. Generally, the inverter cleans and sharpens the active high signal generated. This concept can be reinforced repeating the experiment with an Schmitt trigger NOT gate type: SN74LS14.

 

Using 1uF capacitor and the NOT gate

Fig. 6. Example click waveforms using C = 1 mF. t = R·C = 10 ms. With the NOT gate. The event duration is 2 ms.

Considering the results obtained using a simple RC filter, more elaborated button conditioning circuits using specialised gates (Schmitt trigger) can be inferred, for instance the circuit for the keys in the DE10-Lite board including the SN74LVC2G17 chip (Fig. 7).

And thus, for many applications requiring noise immunity and neat single event detection, additional digital synchronisers and debouncing filters based on FSM such the example presented in this tutorial, has to be included to generate clean digital events from push-buttons.  

DE10-Lite conditioning circuits for keys

Fig. 7. DE10-Lite circuits for debouncing key push-buttons.