UPC EETAC Bachelor's Degree in Telecommunications Systems and in Network Engineering EEL

L4.2

Lecture 3

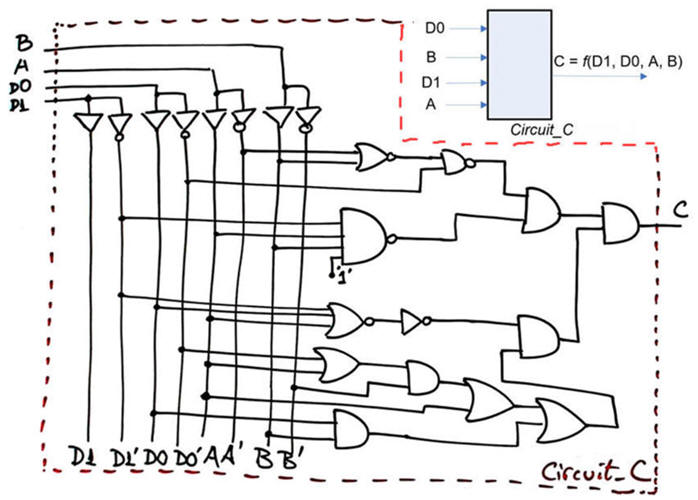
L4.3: How fast is a circuit processing or computing?

[P4]  Power consumption, propagation delay, switching speed

L5.1

[11/10]

We can finish this chapter paying attention again to digital technologies. Digital voltage levels and noise margins were studied in L1.6. Thus, this time we can discuss succinctly about two important features: power consumption and switching speed. We can try to answer the question: How fast is the circuit under design?

1.6.3.4. Current and power consumption.

Currents (pA, nA, μA, mA) and power  consumption (pW, nW, μW, mW)

Powering a logic gate and connecting a switching signal. Example of CMOS_Gates.pdsprj adapting circuit structures proposed in datasheets.

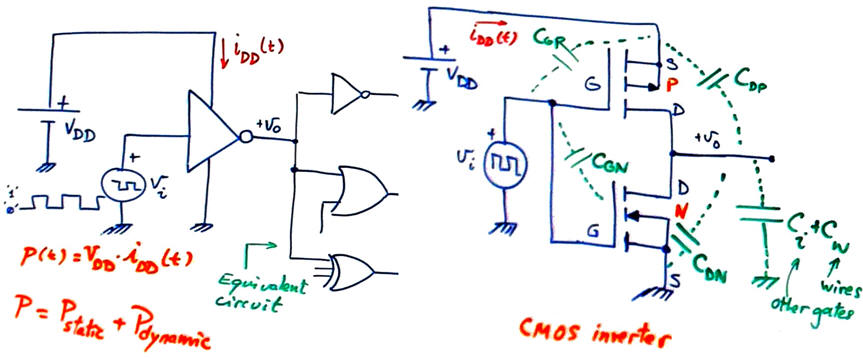CMOS gate

Fig. 1. A single logic NOT gate connected to a pulse generator and to a load composed by several other gates. To make it simple, we will consider ideal input conditions (very high Zin ) and ZL represented by a lumped load capacitor.

Fig.2 shows a NOT transfer function and equivalent circuits in three region. This is a NOT_Gate.pdsprj where you can see how even the input protection circuit can be modelled. It only works when inputs are higher or lower than power rails VDD and GND.

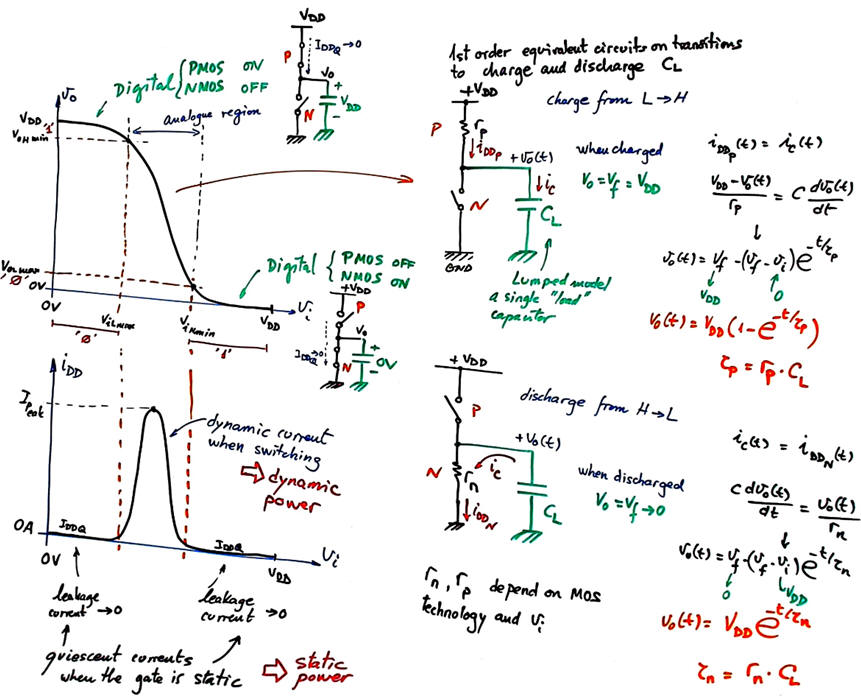CMOS equivalent circuits

Fig. 2. CMOS NOT gate and its transfer function. There is a forbidden (analogue) voltage input band where the gate is transiting between logic levels. Transitions between digital levels will take time because even if there are only parasitic capacitors in the circuit, charging and discarging them cannot be done instantly.

Therefore, the gate can be modelled using three equivalent circuits. Two static circuit with ideal switches ON and OFF, and practically zero current, meaning a very low static power consumption. And a first order equivalent circuit valid for charging and discharging CL in transitions. CL is a modelled lumped component modelling all parasitic capacitatnces at output terminal.

Static power dissipation is the power consumed when the output or input is not switching (or switching at very low frequency). Normally, static power dissipation is caused by leakage current (quiescent current).

CMOS technology has very low static power consumption. Fig. 3 shows data from 4069UB sextuple NOT chip. Typical quiescent current for the device (6 NOT gates) is only 10 nA @ 25°C.

Power static in CMOS

Fig. 3. CMOS IDDQ do not changes on logic values.

Bipolar technologies have a larger static power consumption. Fig. 4 shows data from 74LS04 sextuple NOT chip. Furthermore, quiescent current when the output is high is different from quiescent current when output is low.

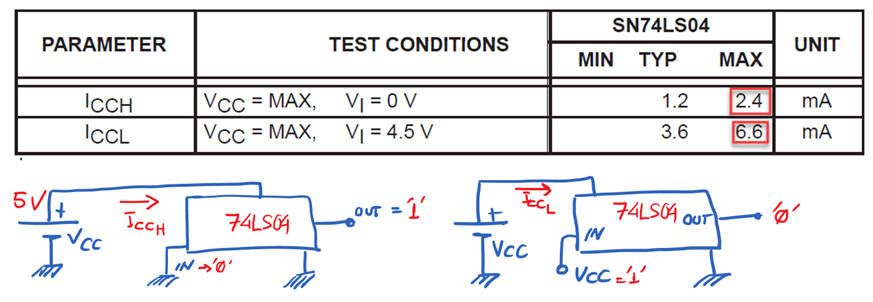static TTL-LS

Fig. 4. TTL-LS ICC depends on the output values. Datasheet shows current consumption ICCH when all (six) inputs are at '0', and ICCL when all (six) inputs are at '1'.

Dynamic power is the power consumed by digital circuits when processing at high speed. For instance, in CMOS technology dynamic power consumption is caused by non-negligible switching currents in transition times when charging and discharging output parasitic capacitors; transistors cannot be modelled as perfect switches with zero seconds switching times, and thus they are not ideal. Moreover, in transitions both NMOS and PMOS transistors are momentarily conducting at the same time at signal edges. The higher the frequency of operation the higher the dynamic power because transition times a preponderant in every period.

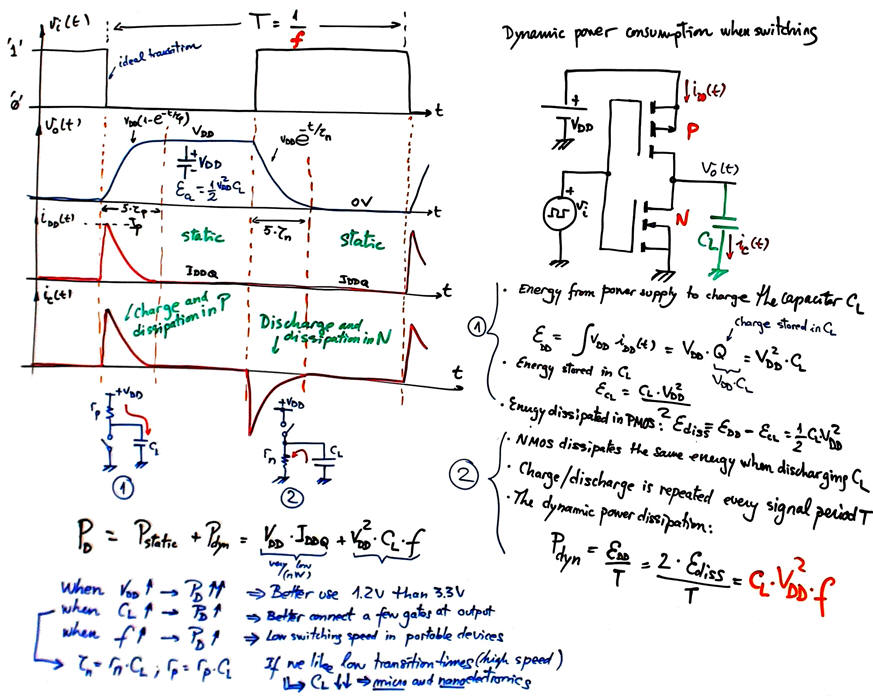Dynamic power consumption

Fig. 5. Analysing currents in one period of signal switching. Calculating the dynamic power consumed by PMOS and NOMS transistors.

We can run Proteus simulations and represent results using CMOS_NOT_switching_LF.pdsprj. For instance, in Fig. 6. there is the circuit running at low frequencies (1 kHz) where tH and tL are predominating over transitions times. Current IDDQ will be very low, in the range of pA or nA.

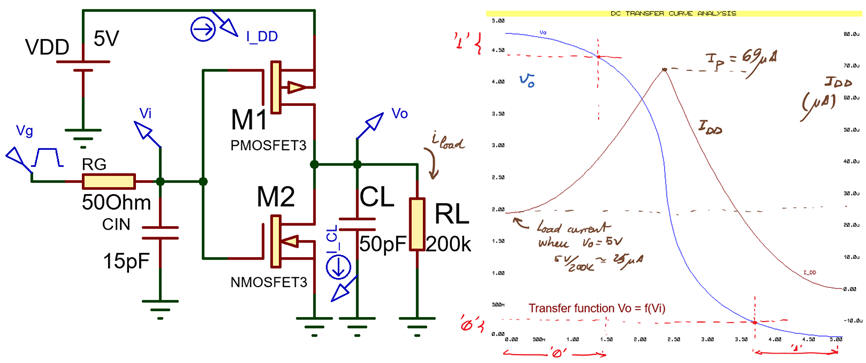Low frequencies. Transfer function
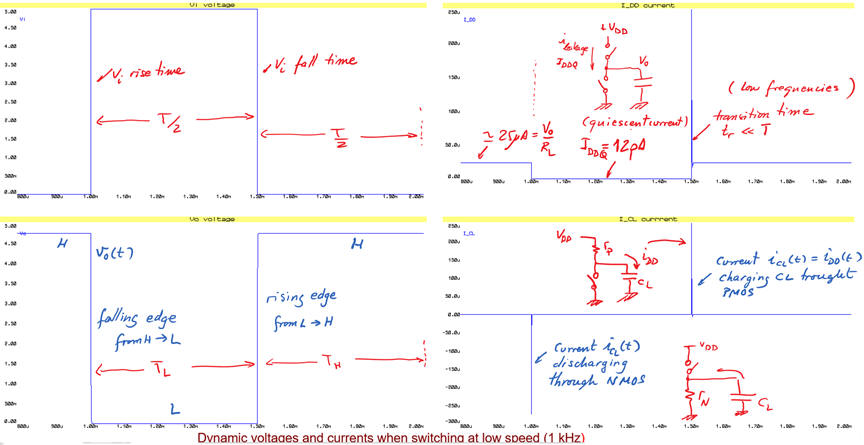Voltages and currents

Fig. 6. Switching the NOT gate at low frequencies. If RL is very high, the average current value over a period is very low because static terms predominate (TH, TL >> tr, tf). Pdyn = CL · VDD^2 · f = 1.25 μW

In Fig. 7. there is the same circuit running at high frequencies (150 kHz) where transition times tPHL and tPLH are very long with respect the period duration. Current IDD will be very high, in the range of μA because the circuit is switching for most of the period.

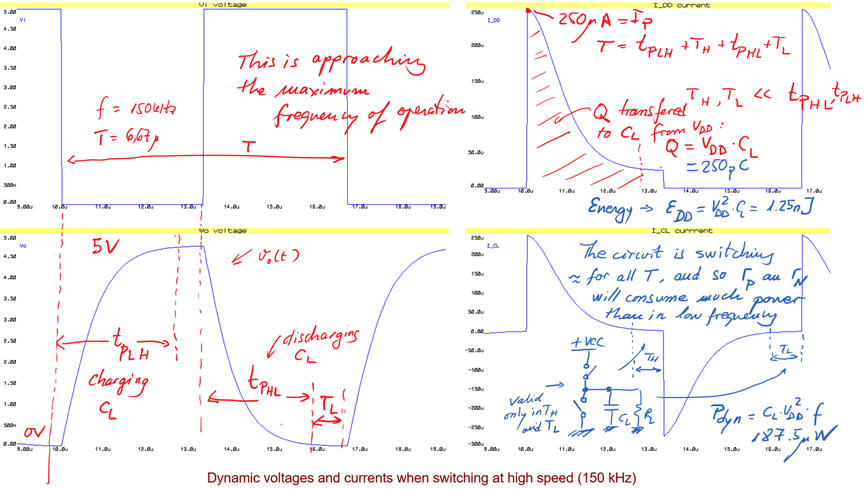High frequency switching

Fig. 7. Switching the NOT gate at high frequencies. The mean current value over a period is high because dynamic terms predominate (TH, TL << tr, tf). Pdyn = CL · VDD^2 · f = 187.5 μW

 

1.6.3.5. Digital circuit propagation time, worst-case scenario: longest propagation delay

Propagation delay (~ns)

Rise and fall times describe the dynamics at the output of a logic element and as shown in Fig. 2 and Fig. 8, the simple first order circuit for charging and discharging CL is a good aproximation.

Propagation delay tP of a signal path is the time required to change the output when a change at the input is produced. It is required studying semiconductor physics to be able to relate output timing to input timing. We will read these parameters from datasheets because the simple first order circuit in Fig. 2 is not enough.

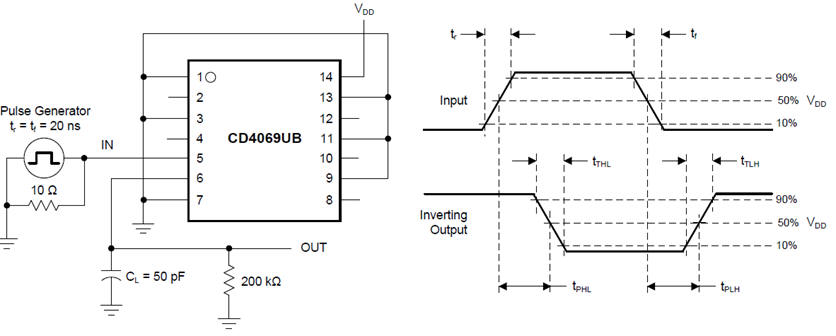CMOS 4069UB dynamic circuit
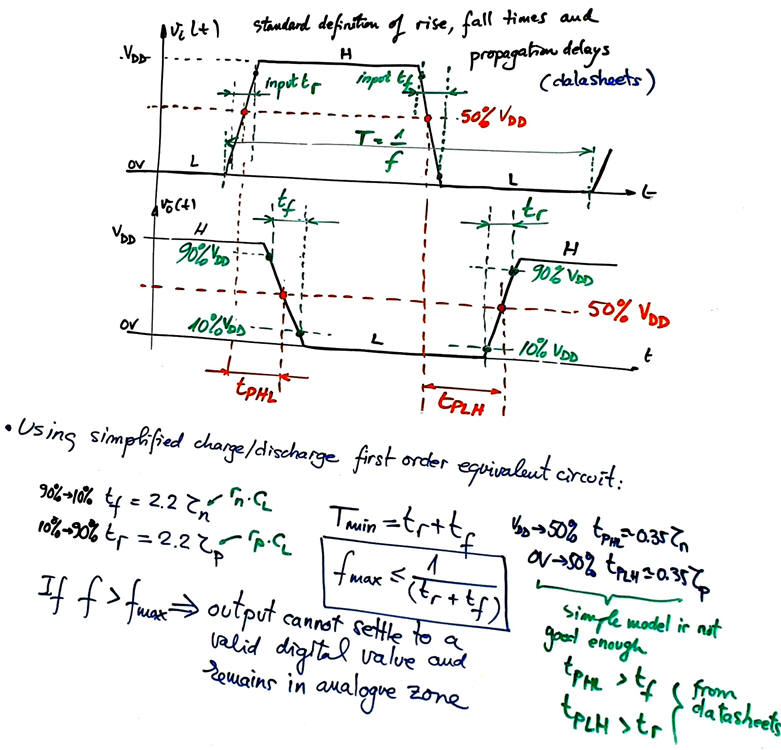Standard propagation time definition

Fig. 8. Propagation delays, rise time and fall time definitions from datasheets. We can use the simplified first order circuit in Fig. 2 to estimate these parameters.

We better rely on datasheet data and represent propagation delay idealising the waveforms for clarity. Every technology has specific propagation delays tPHL and tPLH.

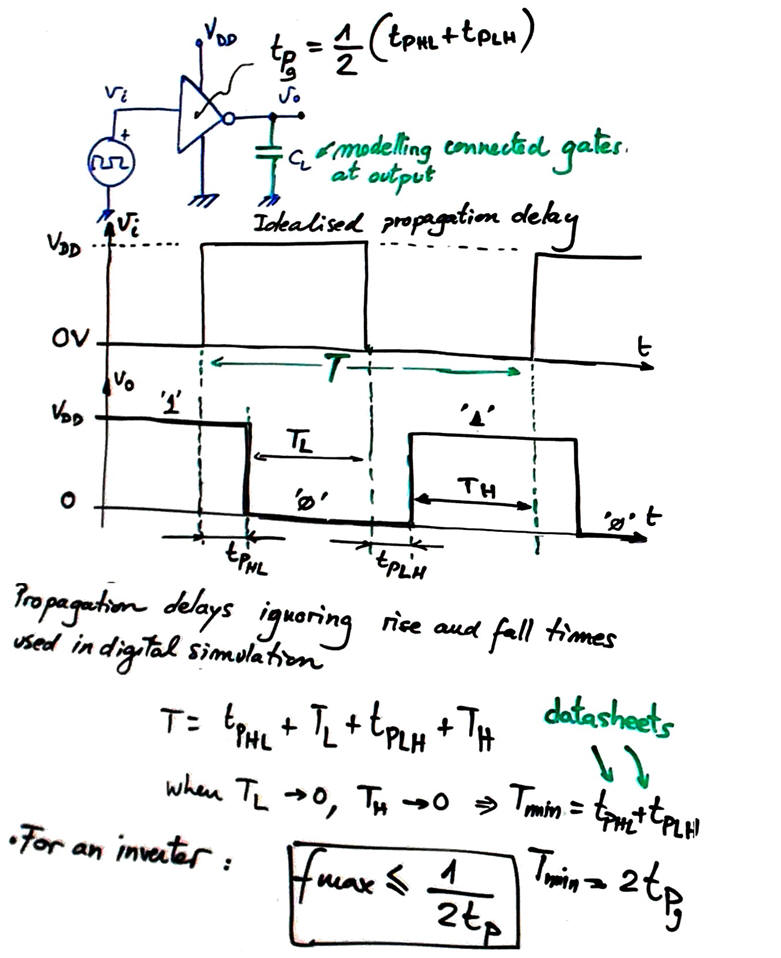Propagation times
4069 switching parameters

Fig. 9. Signals represented without considering rise and fall times, idealing signal transitions and propagation delays. Example of switching parameters from 4069UB CMOS sextuple inverter chip. Test conditions such load capacitor CL modelling loads determine typical values. Higher VDD means shorter delays but higher power consumption.

 

1.6.3.6. How fast is a digital circuit?

Maximum switching speed (~MHz)

As shown in Fig. 7 the NOT gate cannot switch much faster than about 160 kHz, because higher than these frequencies valid digital logic levels are not attained and Tmin = tPHL + tPLH. For a single gate fMAX = 1/(2·tPg)

A digital circuit consist of many levels of gates, and each gate adds a new propagation delay. As represented in Fig. 10, if a circuit has four levels of gates the propagation delay will be four times longer. To simplify the problem in our introductory course we will assume that (unless indicated otherwise) high-to-low tPHL and low-to-high tPLH propagation delays are identical, and also that all gates in a circuit has the same propagation time tPg. In this way we can infer the worst case scenario: the longest propagation signal path. And thus, we can estimate maximum switching speed of the circuit.

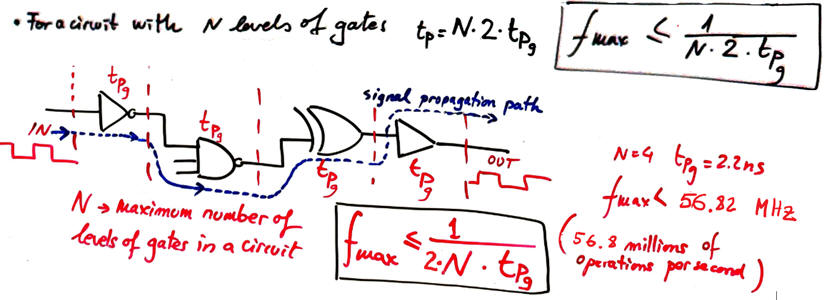Levels of gates
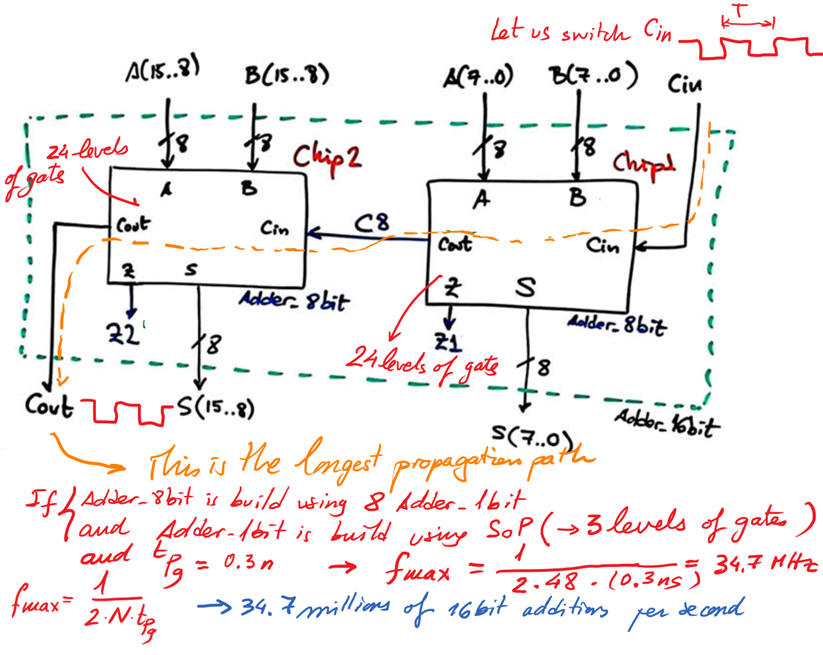Adder_16bit

Fig. 10. Example circuits composed of several levels of gates. Proteus circuit Adder_8bit.pdsprj.

In the analysis below we consider an Adder_32bit in two specific truth table combinations where all bits are switching. Cout is the output that will have the longest propagation delay when switching Cin with a pulse generator.

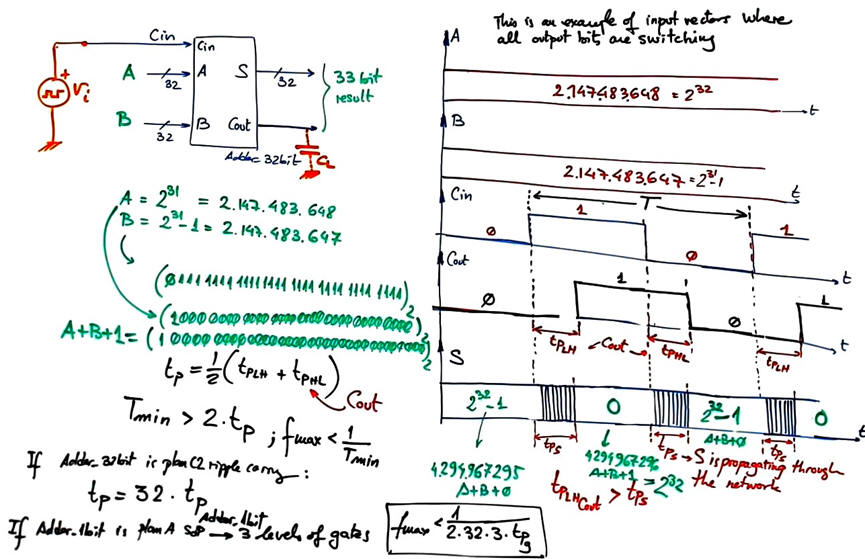Adder_32bit

Fig. 11. Adder_32bit switching. 

Using this Proteus circuit, we can experiment with the Adder_32bit.pdsprj. As we can infer, its propagation delay is four times the propagation delay of the Adder_8bit because is designed simply rippling carry signals.

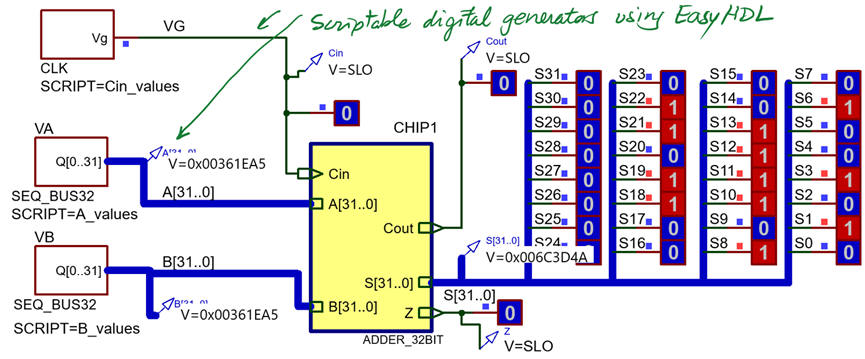Scriptable generators
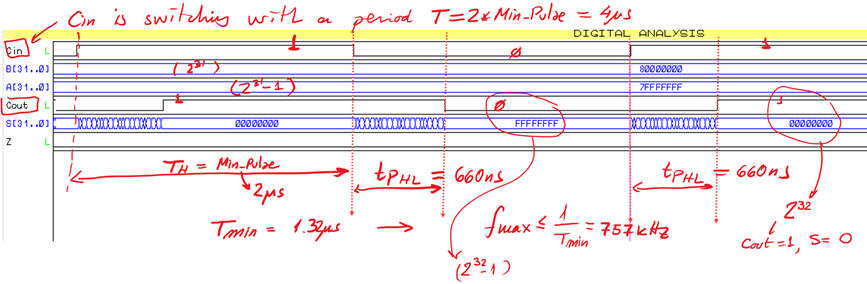Switching Adder_32bit

Fig. 12. Adder_32bit based on TTL-LS technology switching using Proteus and graphical analysis.

Simulation of a CMOS inverter gate 4069 in Proteus.

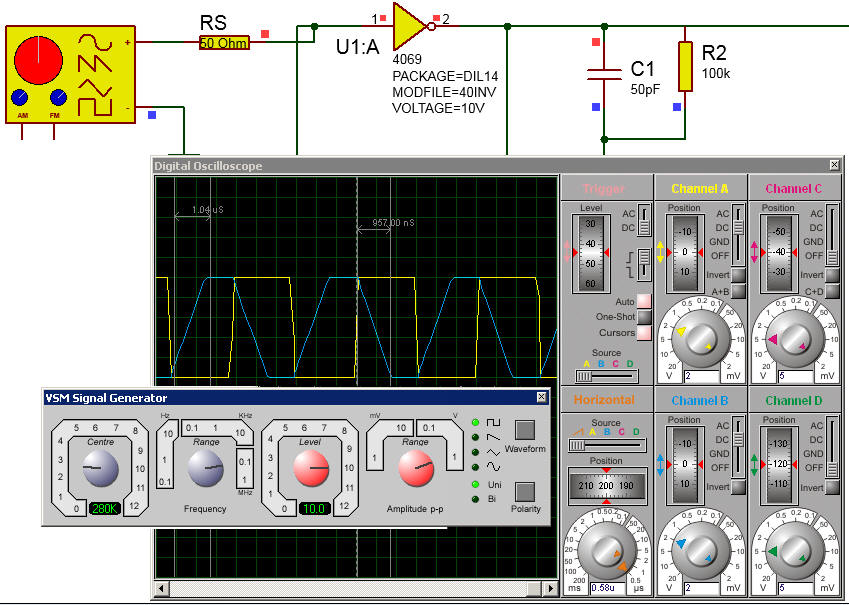Fig.12. Example of a CMOS inverter type 4069 simulated in Proteus.

Simulation of a TTL-LS 74LS04_inverter gate in Proteus.

Example of a simple programmable logic device sPLD solving a function. Maximum speed of operation.

Example of a CPLD electrical characteristics.

Example of a FPGA electrical characteristics.

 

Open collector, open drain gates, definition and how they work

Some logic gates integrated circuits have outputs with open collector or open drain so that the user can define the high digital logic level to glue or interface specific devices or adapt logic families with different voltage margins.

 

1.5.5. Test and verification (technology)

1.5.5.1. Gate-level simulation: propagation delay measurements

Gate-level simulation. How to measure the propagation time for a given target chip: post-synthesis model in VHDL (VHO file and its asociated SDO/SDF delay file) and gate-level VHDL simulation presented in Lab 4.

1.5.5.2. Timing analyser spreadsheet tool: worst-case scenario, longest propagation delay

1.5.5.3. Calculating circuit's maximum speed

Thus, to summarise this lesson, two kind of experiments are possible:

(1) A circuit synthesised for two PLD's: different technologies or different vendors imply different speeds of processing (tPg). For instance an Int_Add_Subt_16bit circuit will generate different processing speeds when synthesised for an Intel or a Xilinx FPGA. Or for an Intel MAX II and for an Intel Cyclone IV.

(2) A circuit planned using different strategies (plans) synthesised for a given PLD. For instance, ripple-carry and carry-lookahead adders will have different speeds of processing. Calculate such parameters for both ripple-carry and carry lookahead 4-bit adders, compare and discuss. As usual, all the necessary files for developing and testing using gate-level simulations and timing analyser tools are in these tutorials in the corresponding sections. 

These ideas on propagation delay and circuit speed calculations will be consolidated at Lab4 tutorials, where we will use both, (1) ModelSim gate-level measurements at a given transition, and (2) calculating the worst-case scenario, the longest propagation time using Quartus Prime timing analyser spreadsheet. 

1.13. Target chips: programmable logic devices (PLD)

Reviewing target chip technologies: programmable logic devices

1.13.1. sPLD (ispGAL22V10) and programmable arrays to implement logic functions

1.13.2. CPLD: complex programmable logic device

1.13.3. FPGA: field programmable gate array

 

Exercise: Calculate how fast is the following circuit. a) Technology LS-TTL; b) technology CMOS (VDD = 5V).

Circuit_C